题目内容
14．
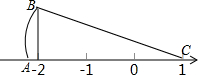如下：已知CA=CB，那么数轴上点A所表示的数是1$-\sqrt{10}$．
分析 首先在直角三角形中，利用勾股定理可以求出线段CB的长度，然后根据CA=CB即可求出CA的长度，接着可以求出数轴上点A所表示的数．
解答 解：∵BC=$\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$，
则CA=BC=$\sqrt{10}$，
则A到原点的距离是$\sqrt{10}$-1，且A在原点左侧．
则点A所表示的数是1-$\sqrt{10}$．
故答案为：$1-\sqrt{10}$．
点评 此题主要考查了实数与数轴之间的对应关系，首先正确根据数在数轴上的位置判断数的符号以及绝对值的大小，再根据运算法则进行判断．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E．B、E是半圆弧的三等分点，弧BE的长为$\frac{2}{3π}$，求图中阴影部分的面积．
