题目内容
16.已知P(x,y)的坐标满足方程|x+1|+$\sqrt{y-2}$=0,则P点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据非负数的性质求出x、y,再根据各象限内点的坐标特征解答.
解答 解:由题意得,x+1=0,y-2=0,
解得x=-1,y=2,
所以,点P(-1,2)在第二象限.
故选B.
点评 本题考查了各象限内点的坐标的符号特征以及非负数的性质,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
7.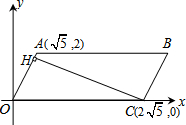 如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
 如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )
如图,在平面直角坐标系中有一平行四边形OABC,已知A($\sqrt{5}$,2),C(2$\sqrt{5}$,0),OA=3,CH⊥OA于H,则下列说法正确的是( )| A. | B点坐标为(2$\sqrt{5}$,2) | B. | B点坐标为(3$\sqrt{5}$,2) | C. | S?OABC=2$\sqrt{5}$ | D. | CH=$\frac{4}{3}$$\sqrt{5}$ |
11.当a<-4时,那么|2-$\sqrt{{{(2+a)}^2}}$|等于( )
| A. | 4+a | B. | -a | C. | -4-a | D. | a |
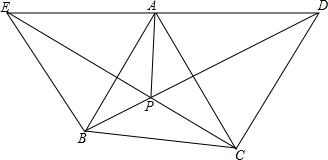 锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.
锐角△ABC中,∠BAC=60°,分别以AB,AC为边向外作正△ABE,△ACD,若AP=4,CP=5,则BP=$\frac{16}{5}$.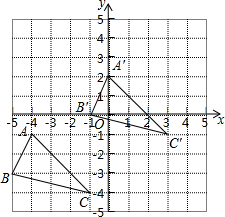 如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2).
如图,直角坐标系中,A(-4,-1),B(-5,-3),C(-1,-4),将△ABC平移,得到△A′B′C′,且点A的对应点A′的坐标为(0,2). 一张长为 a cm,宽为 b cm,周长为32cm的长方形硬纸片,四个角上各剪去一个边长为1cm的小正方形(如图),然后折成一个无盖纸盒(纸板的厚度忽略不计).
一张长为 a cm,宽为 b cm,周长为32cm的长方形硬纸片,四个角上各剪去一个边长为1cm的小正方形(如图),然后折成一个无盖纸盒(纸板的厚度忽略不计).