题目内容
15．解方程组：$\left\{\begin{array}{l}{{a}_{1}+9d=10}\\{{a}_{1}+19d=20}\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{{a}_{1}+9d=10①}\\{{a}_{1}+19d=20②}\end{array}\right.$，
②-①得：10d=10，即d=1，
把d=1代入①得：a1=1，
则方程组的解为$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=1}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
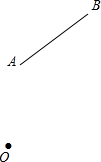如图，点O与线段AB在同一平面内，AO=AB=2，绕点O将线段AB旋转一周，则线段AB扫过的最小面积为4π．
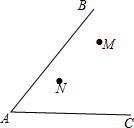如图，南开中学高二年级的学生分别在五云山寨M，N两处参加社会时间活动．先要在道路AB，AC形成的锐角∠BAC内设一个休息区P，使P到两条道路的距离相等，并且使得PM=PN，请用直尺和圆规作出P点的位置（不写作法，值保留作图痕迹）．
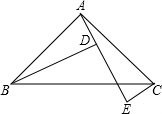已知在△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，BD⊥AE于点D，CE⊥AE于点E．
7．下列各式中，一定能成立的是（ ）
| A． | $\sqrt{{（-2）}^{2}}$=${（-\sqrt{2}）}^{2}$ | B． | $\sqrt{{（\sqrt{7}-3）}^{2}}$=$\sqrt{7}$-3 | C． | $\sqrt{{x}^{2}+2x+1}$=x+1 | D． | $\sqrt{{x}^{2}-25}$=$\sqrt{x+5}$•$\sqrt{x-5}$ |
如图，在⊙O中，弦AB与弦CD相交于E点，$\widehat{ACB}$与$\widehat{DBC}$的度数相等，线段AE与线段DE相等吗？证明你的结论．