题目内容
20.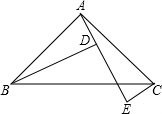 已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,BD⊥AE于点D,CE⊥AE于点E.
已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,BD⊥AE于点D,CE⊥AE于点E.(1)若点B,C在AE的两侧,证明:BD=DE+CE;
(2)若点B,C在AE的同侧,其余条件不变,根据题意作出图形,问:BD,DE,CE之间有何关系?请给予证明.
分析 (1)根据已知利用AAS判定△ABD≌△CAE,从而得到BD=AE,AD=CE,因为AE=AD+DE,所以BD=DE+CE;
(2)BD=DE-CE,根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE,AD=CE,因为AD+AE=BD+CE,所以BD=DE-CE.
解答 解:(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,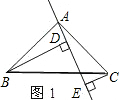
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
$\left\{\begin{array}{l}{∠BDA=∠AEC}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)BD=DE-CE;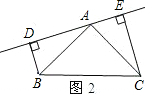
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∴∠ABD+∠DAB=∠DEB+∠CAE,
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
$\left\{\begin{array}{l}{∠BDA=∠AEC}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE-CE.
点评 此题主要考查学生对全等三角形的判定方法的理解及运用,常用的判定方法有SSS,SAS,AAS等.这种类型的题目经常考到,要注意掌握.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
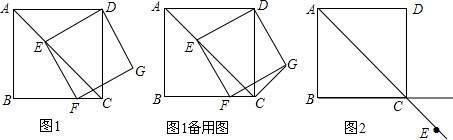
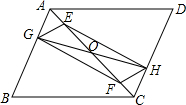 如图所示,已知,在?ABCD中,点E,F在AC上,且AF=CE,点G,H分别在AB,CD上,且AG=CH,AC与GH相交于点O,求证:四边形EGFH是平行四边形.
如图所示,已知,在?ABCD中,点E,F在AC上,且AF=CE,点G,H分别在AB,CD上,且AG=CH,AC与GH相交于点O,求证:四边形EGFH是平行四边形.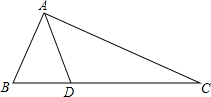 如图,△ABC中,AD是角平分线,且AC=AB+BD,∠C=26°,试求∠B的度数.
如图,△ABC中,AD是角平分线,且AC=AB+BD,∠C=26°,试求∠B的度数.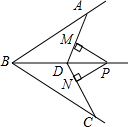 如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M,N分别是垂足,求证:PM=PN.
如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M,N分别是垂足,求证:PM=PN.