题目内容
4. 如图,在⊙O中,弦AB与弦CD相交于E点,$\widehat{ACB}$与$\widehat{DBC}$的度数相等,线段AE与线段DE相等吗?证明你的结论.
如图,在⊙O中,弦AB与弦CD相交于E点,$\widehat{ACB}$与$\widehat{DBC}$的度数相等,线段AE与线段DE相等吗?证明你的结论.
分析 连接AD,由$\widehat{ACB}$=$\widehat{DBC}$,可得$\widehat{AC}$=$\widehat{BD}$,再根据在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等可得AE=DE.
解答  解:∵$\widehat{ACB}$=$\widehat{DBC}$,
解:∵$\widehat{ACB}$=$\widehat{DBC}$,
∴$\widehat{ACB}$-$\widehat{CB}$=$\widehat{DBC}$-$\widehat{CB}$,
∴$\widehat{AC}$=$\widehat{BD}$,
∴AE=DE.
点评 此题主要考查了圆心角、弧、弦的关系,关键是掌握在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
13.已知点A(1,2),AC⊥x轴,垂足为C,则C点的坐标为( )
| A. | (0,0) | B. | (0,2) | C. | (1,0) | D. | (0,1) |
14.若代数式x2+kxy+9y2是完全平方式,则k的值是( )
| A. | 3 | B. | ±3 | C. | 6 | D. | ±6 |
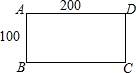 据统计资料,甲、乙两种农作物的单位面积产量的比是1:2,现要把一块长为200m,宽100m的长方形土地分为两部分,分别种植这两种作物,使甲、乙两种作物的总产量的比是3:10
据统计资料,甲、乙两种农作物的单位面积产量的比是1:2,现要把一块长为200m,宽100m的长方形土地分为两部分,分别种植这两种作物,使甲、乙两种作物的总产量的比是3:10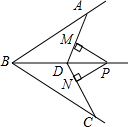 如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M,N分别是垂足,求证:PM=PN.
如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M,N分别是垂足,求证:PM=PN.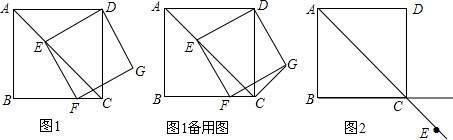
 画出如图三棱柱的三种视图.
画出如图三棱柱的三种视图.