题目内容
2. 如图.已知Rt△ABC中,∠B=90°,∠A=30°,AB=2$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C′位置且A,C,B′共线,则A经过的路线长为( )
如图.已知Rt△ABC中,∠B=90°,∠A=30°,AB=2$\sqrt{3}$,将△ABC绕顶点C顺时针旋转至△A′B′C′位置且A,C,B′共线,则A经过的路线长为( )| A. | 8 | B. | 4$\sqrt{3}$ | C. | $\frac{32}{3}$π | D. | $\frac{8}{3}$π |
分析 点A经过的路线即以C为圆心,以AC的长为半径的弧.利用解直角三角形的知识求得AC的长和∠ACB的度数,从而求得∠ACA′的度数,再根据弧长公式进行计算.
解答 解:在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=2$\sqrt{3}$,
∴∠ACB=60°,AC=$\frac{AB}{cosA}$=4.
∴∠ACA′=120°.
∴点A经过的路线的长度是$\frac{120π•4}{180}$=$\frac{8}{3}$π.
故选D
点评 本题考查旋转变换、弧长公式、解直角三角形等知识,解题的关键是确定点A的运动轨迹,属于中考常考题型.

练习册系列答案
相关题目
13.据海关统计,2016年前两个月,我国进出口总值为37900亿元人民币,将 37900亿用科学记数法表示为( )
| A. | 3.97×1010 | B. | 0.379×1013 | C. | 3.79×1010 | D. | 3.79×1012 |
7.若点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
12.某种商品进货后,零售价定为每件900元,为了适应市场竞争,商店按零售价的九折降价,并让利40元销售,仍可获利25%,问这种商品的进价为多少元?( )
| A. | 610 | B. | 616 | C. | 648 | D. | 680 |
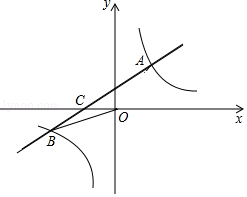 如图,在平面直角坐标系xOy中,一次函数y=ax+b(a,b是常数,且a≠0)的图象与反比例函数$y=\frac{k}{x}$(k是常数,且k≠0)的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
如图,在平面直角坐标系xOy中,一次函数y=ax+b(a,b是常数,且a≠0)的图象与反比例函数$y=\frac{k}{x}$(k是常数,且k≠0)的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.