Question

2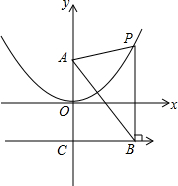．如图，抛物线的顶点在原点O，且过（2，1）点；直线BC∥x轴交y轴于点C，C（0，-1），A（0，1）
（1）求抛物线的解析式；
（2）点P是（1）中抛物线上一点，过点P作BC的垂线，垂足为点B，求证：AB平分∠OAP；
（3）当△PAB是等边三角形时，求P点的坐标．

Answer 1

分析 （1）由抛物线过顶点在原点可设出抛物线解析式，再由点（2，1）可利用待定系数法可求得抛物线解析式；
（2）可设出P点坐标，过P作PH⊥y轴于点H，则可表示出PA的长，再利用条件表示出PB，可证得PA=PB，再结合平行线的性质证明∠PAB=∠OAB，可证得结论；
（3）由等边三角形的性质可求得∠ABC=30°，则可求得AB的长，结合（2）中PA=PB=AB，则可求得P点的坐标，

解答 解：
（1）∵抛物线的顶点在原点O，且过（2，1）点，
∴可设抛物线解析式为为y=ax²，
∴a=$\frac{1}{4}$，
∴二次函数的解析式为y=$\frac{1}{4}$x²；
（2）证明：
∵点P在抛物线y=$\frac{1}{4}$x²上，
∴可设点P的坐标为（x，$\frac{1}{4}$x²），
如图，过点P作PH⊥y轴于点H，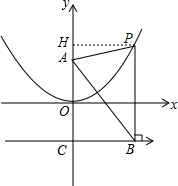

则HA=$\frac{1}{4}$x²-1，PH=x，
∴Rt△PHA中，PA=$\sqrt{（\frac{1}{4}{x}^{2}-1）^{2}+{x}^{2}}$=$\frac{1}{4}$x²+1，
∵PB⊥BC于B，
∴PB=$\frac{1}{4}$x²+1，
∴PA=PB，
∴∠PAB=∠PBA，
又∵PB∥x轴，
∴∠OAB=∠PBA，
∴∠OAB=∠PAB，
∴AB平分∠OAP；
（3）解：当△PAB是等边三角形时，∠PBA=60°，
∴∠ABC=30°，
在Rt△ABC中，AB=2AC=2×2=4，
∵PA=PB=AB，
∴$\frac{1}{4}$x²+1=4，解得：x=±2$\sqrt{3}$，
∴$\frac{1}{4}$x²=$\frac{1}{4}$×12=3，
∴满足条件的点P的坐标为（2$\sqrt{3}$，3）或（-2$\sqrt{3}$，3）．

点评 本题主要考查二次函数的综合应用，涉及知识点有待定系数法、勾股定理、平行线的性质、角平分线的判定及等边三角形的性质等．在（1）中需要注意待定系数法的应用步骤，在（2）中用P点表示出PA和PB的长是解题的关键，在（3）中利用等边三角形的性质列出方程是解题的关键．本题考查知识点较多，综合性较强，难度适中．