题目内容
12.(1)如图①,△ABC是等边三角形,以BC为直径的⊙O分别交AB、AC于点D、E.判断△DOE的形状.并说明理由.(2)将(1)中的条件“△ABC是等边三角形”,改为“在△ABC中,∠A=60°”,其余条件不变(如图②),(1)中的结论还成立吗?

分析 (1)由△ABC为等边三角形,可得∠B=∠C=60°.又由OB=OC=OD=OE,即可证得△OBD,△OEC均为等边三角形,继而证得△ODE是等边三角形;
(2)首先连接CD,由BC为⊙O直径,可得∠BDC=90°,继而求得∠DOE=60°,则可证得结论.
解答 (1)△ODE为等边三角形.
证明:∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵OB=OC=OD=OE,
∴△OBD,△OEC均为等边三角形.
∴∠BOD=∠COE=60°.
∴∠DOE=60°.
∵OD=OE,
∴△ODE为等边三角形.
故答案为:等边三角形.
(2)成立.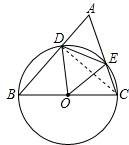
证明:如图,连接CD,
∵BC为⊙O直径,
∴∠BDC=90°,
∴∠ADC=90°.
∵∠A=60°,
∴∠ACD=30°.
∴∠DOE=60°,
∵OD=OE,
∴△DOE为等边三角形.
点评 此题考查了圆周角定理以及等边三角形的判定与性质,此题比较适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
2.下列命题,为假命题的是( )
| A. | 内错角不相等,两直线不平行 | B. | 一个角的余角一定大于这个角 | ||
| C. | 一个钝角的补角必是锐角 | D. | 过两点有且只有一条直线 |
7.下列各组数据能作为一个等腰三角形各边长的是( )
| A. | 1,1,2 | B. | 4,2,4 | C. | 2,3,4 | D. | 3,3,7 |
 如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.
如图,在平面直角坐标系中,已知等边△OAB的顶点A在反比例函数y=$\frac{4\sqrt{3}}{x}$(x>0)图象上,当等边△OAB的顶点B在坐标轴上时,求等边△OAB顶点A的坐标和△OAB的面积.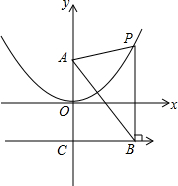 如图,抛物线的顶点在原点O,且过(2,1)点;直线BC∥x轴交y轴于点C,C(0,-1),A(0,1)
如图,抛物线的顶点在原点O,且过(2,1)点;直线BC∥x轴交y轴于点C,C(0,-1),A(0,1)