题目内容
20. 如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,AC=BC,AE⊥AB,BF⊥AB,且∠ECF=45°.若AE=$\sqrt{2}$,BF=$\sqrt{10}$,则EF的长为2$\sqrt{3}$.
分析 作ED⊥BF于D,由已知条件和等腰直角三角形的性质得出∠CAE=∠FBC,证出∠1=∠2,得出△ACE∽△BFC,由相似三角形的对应边成比例得出AC•BC=AE•BF=AC2,求出AC2=2$\sqrt{5}$,得出DE2=4$\sqrt{5}$,由勾股定理求出EF即可.
解答 解:作ED⊥BF于D,如图所示: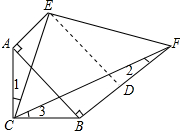
∵∠ECF=45°,∠ACB=90°,
∴∠1+∠3=45°,
∵AC=BC,
∴∠ABC=∠CAB=45°,
∵AE⊥AB,BF⊥AB,
∴∠EAB=∠ABF=90°,
∴∠CAE=45°+90°=135°=∠FBC,
∴∠2+∠3=45°,
∴∠1=∠2,
∴△ACE∽△BFC,
∴$\frac{AC}{BF}=\frac{AE}{BC}$,
∴AC•BC=AE•BF=AC2,
∴AC2=$\sqrt{2}$×$\sqrt{10}$=2$\sqrt{5}$,
∴DE2=AB2=2AC2=4$\sqrt{5}$,
∴EF=$\sqrt{D{E}^{2}+D{F}^{{\;}^{2}}}$=$\sqrt{4\sqrt{5}+(\sqrt{10}-\sqrt{2})^{2}}$=2$\sqrt{3}$;
故答案为:2$\sqrt{3}$.
点评 本题考查了等腰直角三角形的性质、相似三角形的判定与性质、勾股定理;由三角形相似得出AC2的值是解决问题的关键.

练习册系列答案
相关题目
10.在平面直角坐标系中有一个矩形ABCD,点A的坐标为(-2,1),点B的坐标为(2,1),点D的坐标为(-2,-1),现将以矩形为原点O为位似中心,位似比为3:1,将矩形ABCD扩大,得到新的四边形A1B1C1D1,则点C1的坐标为( )
| A. | (6.-3) | B. | (-3,6) | C. | (6,3) | D. | (3,6) |
9.一文具店的装订机的价格比文具盒的价格的3倍少1元,购买2把装订机和6个文具盒共需70元,问装订机与文具盒价格各是多少元?设文具盒的价格为x元,装订机的价格为y元,依题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{3x-y=1}\\{6x+2y=70}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-3x=1}\\{6x+2y=70}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-3x=1}\\{2x+6y=70}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x-y=1}\\{2x+6y=70}\end{array}\right.$ |
 如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°.
如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°. 如图,D、E是AB的三等分点,DF∥EG∥BC,则图中三部分面积S1:S2:S3=1:3:5.
如图,D、E是AB的三等分点,DF∥EG∥BC,则图中三部分面积S1:S2:S3=1:3:5. 如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.
如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.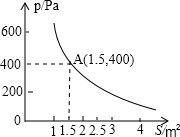 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.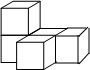 如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由五个小正方体组合而成的,它的左视图是( )