题目内容
分式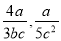 的最简公分母是_________.
的最简公分母是_________.
 15bc2
【解析】试题分析:分式与的最简公分母是15bc2.
故答案为:15bc2.
15bc2
【解析】试题分析:分式与的最简公分母是15bc2.
故答案为:15bc2.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案在□ABCD中,AB≠AD,满足下列条件,不一定能构成平行四边形的是( )
A. 四个内角平分线围成的四边形
B. 过四个顶点作对边的高线围成的四边形
C. 以对角线的交点把对角线分成的四部分的中点为顶点的四边形
D. 以一条对角线上的两点,与另两个顶点为顶点的四边形.
 D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D.
D
【解析】【解析】
∵?ABCD的四个内角平分线围成的四边形是平行四边形,∴选项A正确;
∵过?ABCD四个顶点作对边的高线围成的四边形是平行四边形,∴选项B正确;
∵以?ABCD各边中点为顶点的四边形是平行四边形,∴选项C正确;
∵以?ABCD一条对角线上的两点与另两个顶点为顶点的四边形不一定是平行四边形,∴选项D不正确.
故选D. 如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
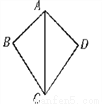
 2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2.
2
【解析】根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为:2. 计算
(1) (2)
(2)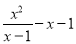
(3)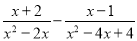 (4)
(4)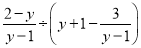
 (1);(2);(3);(4).
【解析】试题分析:(1)同分母分式相减,分母不变,把分子相减,最后结果化成最简即可;
(2)把整式看成是分母为1的分式,通分后把分子相减即可;
(3)把两个分母分解因式后通分,再利用同分母分式减法法则进行计算即可;
(4)把括号内的分式通分相减,化成最简后,再把除法转化为乘法,分母分解因式后再进行约分即可.
试题解析:
【解析】...
(1);(2);(3);(4).
【解析】试题分析:(1)同分母分式相减,分母不变,把分子相减,最后结果化成最简即可;
(2)把整式看成是分母为1的分式,通分后把分子相减即可;
(3)把两个分母分解因式后通分,再利用同分母分式减法法则进行计算即可;
(4)把括号内的分式通分相减,化成最简后,再把除法转化为乘法,分母分解因式后再进行约分即可.
试题解析:
【解析】... 当分式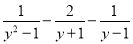 的值等于零时,则y=_________.
的值等于零时,则y=_________.
 【解析】试题分析:当分式的值等于零时,
=0,
去分母得:1-2(y-1)-(y+1)=0,
解得:y=,
当y=时y2-1≠0,
所以y=是分式方程的解,
故答案为: .
【解析】试题分析:当分式的值等于零时,
=0,
去分母得:1-2(y-1)-(y+1)=0,
解得:y=,
当y=时y2-1≠0,
所以y=是分式方程的解,
故答案为: . 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在封闭图形ABCD附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),
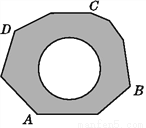
记录如下:
掷小石子所落的总次数 小石子所落的有效区域 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 14 | 48 | 89 | … |
小石子落在圆以外的阴影部分(含外缘)的次数n | 30 | 95 | 180 | … |
(1)当投掷的次数很大时,m∶n的值越来越接近___________(结果精确到0.1);
(2)若以小石子所落的有效区域里的次数为总数(即m+n),则随着投掷次数的增加,小石子落在圆内(含圆上)的频率稳定在___________附近;
(3)若你投一次石子,则小石子落在圆内(含圆上)的概率为___________;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
 (1)0.5;(2);(3);(4)3π m2
【解析】试题分析:根据表格中提供的数据计算出落在圆内的概率与落在阴影内的概率的比值,即可解答.
试题解析:(1)0.5, ≈0.5, ≈0.5, ≈0.5,所以m:n的值越来越接近0.5,
(2) 由(1)可得≈.
(3)
(4)S圆=π×12=π(m2),而≈,
所以S封闭图形ABCD≈3π m2.
(1)0.5;(2);(3);(4)3π m2
【解析】试题分析:根据表格中提供的数据计算出落在圆内的概率与落在阴影内的概率的比值,即可解答.
试题解析:(1)0.5, ≈0.5, ≈0.5, ≈0.5,所以m:n的值越来越接近0.5,
(2) 由(1)可得≈.
(3)
(4)S圆=π×12=π(m2),而≈,
所以S封闭图形ABCD≈3π m2. 某收费站在2 h内对经过该站的机动车统计如下表:
类型 | 轿车 | 货车 | 客车 | 其他 |
数量/辆 | 36 | 24 | 8 | 12 |
若有一辆机动车经过这个收费站,利用上面的统计表估计它是轿车的概率为( )
A.  B.
B. 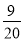 C.
C. 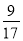 D.
D. 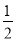
 B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B.
B
【解析】由图表可得出,轿车的数量为:36,机动车的数量为:36+24+2+12=80,所以轿车的概率为: ,故选:B. 如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
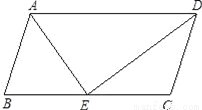
 (1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中...
(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中... 如图,在?ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为__.
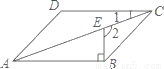
 110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°.
110°.
【解析】根据平行四边形的性质可得AB∥CD,根据平行线的性质可得∠1=∠CAB=20°,因BE⊥AB,可得∠EBA=90°,所以∠2=∠EBA+∠CAB=90°+20°=110°. 
