题目内容
11.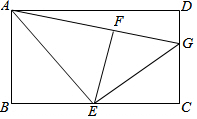 如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.(1)求证:GF=GC;
(2)若AB=3,AD=4,求线段GC的长.
(3)我们学过的菱形(填“平行四边形”、“矩形”或“菱形”)的中点四边形一定是矩形;矩形(填“平行四边形”、“矩形”或菱形“)的中点四边形一定是菱形.
分析 (1)连接GE,根据点E是BC的中点以及翻折的性质可以求出BE=EF=EC,然后利用“HL”证明△GFE和△GCE全等,根据全等三角形对应边相等即可得证;
(2)设GC=x,表示出AG、DG,然后在Rt△ADG中,利用勾股定理列式进行计算即可得解;
(3)根据对角线互相垂直的四边形的中点四边形是矩形,以及对角线相等的四边形的中点四边形是菱形进行判断即可.
解答 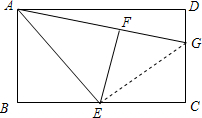 解:(1)连接GE,
解:(1)连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,
$\left\{\begin{array}{l}{EG=EG}\\{EF=EC}\end{array}\right.$,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
(2)设GC=x=FG,则DG=3-x,
∵AF=AB=3,
∴AG=3+x,
在Rt△ADG中,由勾股定理得,42+(3-x)2=(3+x)2,
解得x=$\frac{4}{3}$,
即线段GC的长为$\frac{4}{3}$;
(3)根据菱形的对角线互相垂直,可知菱形的中点四边形一定是矩形;
根据矩形的对角线相等,可知矩形的中点四边形一定是菱形.
故答案为:菱形,矩形.
点评 本题考查了矩形的性质,全等三角形的判定与性质,勾股定理的应用,翻折的性质以及中点四边形的综合应用,找出三角形全等的条件EF=EC是解题的关键.解题时注意:对角线互相垂直的四边形的中点四边形是矩形,以及对角线相等的四边形的中点四边形是菱形.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.下列计算正确的是( )
| A. | (-5)0=0 | B. | x2+x3=x5 | C. | 2a2•a-1=2a | D. | (ab2)3=a2b5 |
19.“五•一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.使代数式$\frac{2x}{x-2}$有意义的x的取值范围为( )
| A. | x>2 | B. | x≠0 | C. | x<2 | D. | x≠2 |
1.抛物线y=2(x+3)2-2的顶点坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |