题目内容
2.已知AB是半径为10厘米的⊙O中一弦,交半径为2$\sqrt{7}$的同心圆于C、D两点,已知圆心O到AB的距离为2cm,则AC+DB=4$\sqrt{6}$.分析 过O作OE⊥CD于E,根据垂径定理证出AC=BD,由勾股定理求出AE、CE的长度,AC的长度也就不难求出,即可得出结果.
解答 解:过O作OE⊥AB,垂足为E,连接OA、OC,如图所示: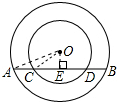
根据垂径定理得:AE=BE=$\frac{1}{2}$AB,CE=DE=$\frac{1}{2}$CD,
∴AC=BD,
∵AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{1{0}^{2}-{2}^{2}}$=4$\sqrt{6}$,CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{(2\sqrt{7})^{2}-{2}^{2}}$=2$\sqrt{6}$,
∴AC=AE-CE=4$\sqrt{6}$-2$\sqrt{6}$=2$\sqrt{6}$,
∴AC+BD=4$\sqrt{6}$;
故答案为:4$\sqrt{6}$.
点评 本题主要考查了垂径定理、勾股定理;作辅助线由垂径定理证出AC=BD是解题的突破口.

练习册系列答案
相关题目
17.若点(-2,y1),(1,y2),(3,y3)都在反比例函数$y=-\frac{6}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
7.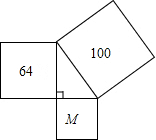 如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
 如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )
如图,三个正方形围成一个直角三角形,64、100分别为所在正方形的面积,则图中字母所代表的正方形的边长是( )| A. | 36 | B. | $4\sqrt{41}$ | C. | 6 | D. | 164 |
14.下列说法正确的是( )
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 有一个角是直角的菱形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
11.已知3a=3b-4,则代数式3a2-6ab+3b2-4的值为( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | 2 | D. | 3 |

 如图,在△ABC中,∠C=90°,AC=BC=4,CD=1,点E为斜边AB上动点,连接CE、DE,则△CDE周长的最小值是6.
如图,在△ABC中,∠C=90°,AC=BC=4,CD=1,点E为斜边AB上动点,连接CE、DE,则△CDE周长的最小值是6.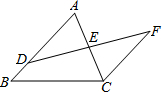 如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.求证:AB=CF+BD.
如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.求证:AB=CF+BD.