题目内容
4. 如图,正六边形ABCDEF的边长为2,则该六边形的面积为( )
如图,正六边形ABCDEF的边长为2,则该六边形的面积为( )| A. | 3$\sqrt{3}$ | B. | 7.5 | C. | 6$\sqrt{3}$ | D. | 10 |
分析 连接OE、OD,由正六边形的特点求出判断出△ODE的形状,作OH⊥ED于H,由特殊角的三角函数值求出OH的长,利用三角形的面积公式即可求出△ODE的面积,进而可得出正六边形ABCDEF的面积.
解答 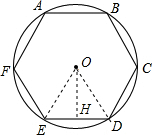 解:连接OE、OD,如图所示:
解:连接OE、OD,如图所示:
∵六边形ABCDEF是正六边形,
∴∠DEF=120°,
∴∠OED=60°,
∵OE=OD=2,
∴△ODE是等边三角形,
作OH⊥ED于H,则OH=OE•sin∠OED=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴S△ODE=$\frac{1}{2}$DE•OH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴S正六边形ABCDEF=6S△ODE=6$\sqrt{3}$.
故选:C.
点评 本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质;根据题意作出辅助线,构造出等边三角形是解答此题的关键.

练习册系列答案
相关题目
19.某同学用描点法y=ax2+bx+c的图象时,列出了表:
由于粗心,他算错了其中一个y值,则这个错误的y值是-5.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
9.直线l外一点P与直线l上两点的连线段长分别为3cm,5cm,则点P到直线l的距离是( )
| A. | 不超过3cm | B. | 3cm | C. | 5cm | D. | 不少于5cm |
13.如果4a=5b(ab≠0),那么下列比例式变形正确的是( )
| A. | $\frac{5}{a}=\frac{4}{b}$ | B. | $\frac{a}{4}=\frac{b}{5}$ | C. | $\frac{a}{b}=\frac{4}{5}$ | D. | $\frac{4}{a}=\frac{b}{5}$ |
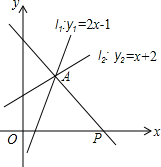 如图,直线l1:y1=2x-1与直线l2:y2=x+2相交于点A,点P是x轴上任意一点,直线l3是经过点A和点P的一条直线.
如图,直线l1:y1=2x-1与直线l2:y2=x+2相交于点A,点P是x轴上任意一点,直线l3是经过点A和点P的一条直线. 如图,画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.
如图,画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.