题目内容
19.先化简再求值:$\frac{{{x^2}-2x+1}}{{{x^2}-1}}÷\frac{x-1}{{{x^2}+x}}-2x$,选择一个你喜欢的值代入求值.分析 原式第一项利用除法法则变形,约分后再合并同类项,得到最简结果,求出x的值代入计算即可求出值.
解答 解:$\frac{{{x^2}-2x+1}}{{{x^2}-1}}÷\frac{x-1}{{{x^2}+x}}-2x$
=$\frac{(x-1)^{2}}{(x+1)(x-1)}$×$\frac{x(x+1)}{x-1}$-2x
=x-2x
=-x,
当x=2时,原式=-2.
点评 本题主要考查了分式的化简求值问题,在解题时要先进行因式分解,再化简.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.甲、乙、丙三人沿圆形操场的某一个固定点出发,甲按顺时针方向走,乙与丙按逆时针方向走,甲第一次遇到乙后又走了30秒遇到丙,再过4分钟第二次遇到乙,已知甲、乙的速度比是3:2,操场的周长是900米,丙的速度是( )米/分.
| A. | 120 | B. | 80 | C. | 60 | D. | 50 |
7.关于x的方程x2+2kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
8.若∠A、∠B为△ABC中的锐角,且$\sqrt{2sinA-\sqrt{3}}$+(cosB-$\frac{1}{2}$)2=0,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 无法确定 |
 如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.
如图,点A、B、C顺次在直线l上,点M是线段AC的中点,点N是线段BC的中点,NC=2cm,AB=8cm,求AM的长.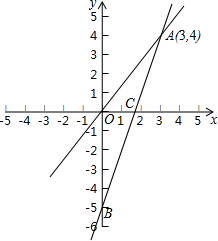 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C. 已知:A、B、C、D四点均在⊙O上,点E在CD的延长线上,AB=AC.求证:DA平分∠BDE.
已知:A、B、C、D四点均在⊙O上,点E在CD的延长线上,AB=AC.求证:DA平分∠BDE.