题目内容
12.泰新高速公路养护小组,乘车沿东西方向的公路检修线路,约定向东为正,早晨从A地出发,晚上到达B地,行走记录为(单位:千米):-7,+9,-2,+8,+6,+9,-5,-1,-7.
(1)B地在A地的哪一边,距离A地多远?
(2)养护过程中,最远处离出发点多远?
(3)若每千米汽车耗油量为0.2升,求该天耗油多少升?
分析 (1)求出-7,+9,-2,+8,+6,+9,-5,-1,-7的和是多少,即可推得B地在A地的哪一边,距离A地多远.
(2)分别求出出发后与A点的距离各为多少,即可推得养护过程中,最远处离出发点多远.
(3)用每千米汽车耗油量乘行驶的路程,求出该天耗油多少升即可.
解答 解:(1)(-7)+(+9)+(-2)+(+8)+(+6)+(+9)+(-5)+(-1)+(-7)=10,
∴B地在A地的东边,距离A地10千米.
(2)|-7|=7,
|(-7)+(+9)|=2,
|(-7)+(+9)+(-2)|=0,
|(-7)+(+9)+(-2)+(+8)|=8,
|(-7)+(+9)+(-2)+(+8)+(+6)|=14,
|(-7)+(+9)+(-2)+(+8)+(+6)+(+9)|=23,
|(-7)+(+9)+(-2)+(+8)+(+6)+(+9)+(-5)|=18,
|(-7)+(+9)+(-2)+(+8)+(+6)+(+9)+(-5)+(-1)|=17,
|(-7)+(+9)+(-2)+(+8)+(+6)+(+9)+(-5)+(-1)+(-7)|=10,
∴出发后与A点的距离分别为:7、2、0、8、14、23、18、17、10,
∴养护过程中,最远处离出发点23千米.
(3)0.2×(|-7|+|+9|+|-2|+|+8|+|+6|+|+9|+|-5|+|-1|+|-7|)
=0.2×54
=10.8(升)
答:若每千米汽车耗油量为0.2升,该天耗油10.8升.
点评 此题主要考查了正数和负数,以及绝对值的含义和求法,要熟练掌握.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
2.用配方法解一元二次方程x2-6x-1=0时,方程可变形为( )
| A. | (x-3)2=10 | B. | (x-6)2=37 | C. | (x-3)2=4 | D. | (x-3)2=1 |
3.下列说法正确的是( )
| A. | 1的平方根是1 | B. | -3是$\sqrt{(-3)^{2}}$的平方根 | ||
| C. | $\sqrt{2}$是2的平方根 | D. | -1的立方根是-1 |
20.在平面直角坐标系中,已知点P的坐标是(3,4),点P与点Q关于y轴对称,则点Q的坐标是( )
| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
 如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.
如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,求当CF⊥AD时,OE的长为1.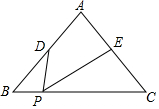 △ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4.
△ABC中,AB=AC=4,BC=5,点D是边AB的中点,点E是边AC的中点,点P是边BC上的动点,∠DPE=∠C,则BP=1或4. 如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积.
如图,有一块四边形的土地,∠D=90°,AB=20m,BC=25m,CD=12m,AD=9m,求该四边形土地ABCD的面积. 如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.
如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.