题目内容
7. 如图,AB=BC=CD=1,CE=2,B、C、E三点共线,BE⊥AB,CD⊥BE,则∠AED=45°.
如图,AB=BC=CD=1,CE=2,B、C、E三点共线,BE⊥AB,CD⊥BE,则∠AED=45°.
分析 连结AE,延长AB,过D点作DF⊥AB于F.先根据勾股定理得到AD,DE,AE,再根据勾股定理的逆定理可得∠ADE=90°,再根据等腰直角三角形的性质即可求解.
解答 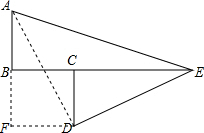 解:连结AE,延长AB,过D点作DF⊥AB于F.
解:连结AE,延长AB,过D点作DF⊥AB于F.
∵AB=BC=CD=1,CE=2,
∴AF=2,DF=1,BE=2+1=3,
在Rt△AFD中,AD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
在Rt△DCE中,DE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
在Rt△AFBE中,AE=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,
∴∠ADE=90°,
∴∠AED=45°.
故答案为:45°.
点评 此题考查了勾股定理,勾股定理的逆定理,等腰直角三角形的性质,关键是证明∠ADE=90°.

练习册系列答案
相关题目
15.某水果商行计划购进A、B两种水果共200箱,这两种水果的进价、售价如下表所示:
(1)若该商行进贷款为1万元,则两种水果各购进多少箱?
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的$\frac{1}{3}$,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
| 价格 类型 | 进价(元/箱) | 售价(元/箱) |
| A | 60 | 70 |
| B | 40 | 55 |
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的$\frac{1}{3}$,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
2. 如图所示的立体图形的俯视图是( )
如图所示的立体图形的俯视图是( )
 如图所示的立体图形的俯视图是( )
如图所示的立体图形的俯视图是( )| A. |  | B. |  | C. |  | D. |  |