题目内容
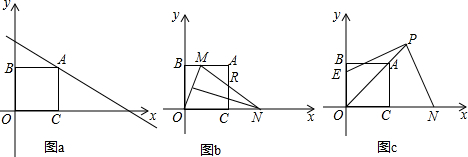
如图(a),在平面直角坐标系中,A为直线y=-
x+3上的一点,AB⊥y轴,AC⊥x轴,四边形ABOC为正方形
(1)求A点的坐标;
(2)如图(b),M为AB边上的一个动点,OM的中垂线交x轴于N,连接MN交AC于点R,求△AMR的周长;
(3)如图(c),若点P为射线OA上任意一点,过P作直线PE、PF,分别与坐标轴交于点E、F(OF>OE),PE⊥PF,求证:OE+OF=
OP.
| 1 |
| 2 |
(1)求A点的坐标;
(2)如图(b),M为AB边上的一个动点,OM的中垂线交x轴于N,连接MN交AC于点R,求△AMR的周长;
(3)如图(c),若点P为射线OA上任意一点,过P作直线PE、PF,分别与坐标轴交于点E、F(OF>OE),PE⊥PF,求证:OE+OF=
| 2 |

考点:一次函数综合题
专题:
分析:(1)A是正方形ABOC的顶点,则横纵坐标相等,再根据在直线y=-
x+3上,即可求解;
(2)设M的横坐标是m,则M的坐标是(2m,2),把m当作已知数,利用待定系数法求得OM的中垂线的解析式,则R的坐标可利用m表示出来,然后利用勾股定理求得MR的长,则三角形的周长即可求得;
(3)作PM⊥x轴于点M,作PN⊥y轴于点N,证明△PNE≌△PMF,证得ME=MF,则OE+OF=OM+ON=
OP.
| 1 |
| 2 |
(2)设M的横坐标是m,则M的坐标是(2m,2),把m当作已知数,利用待定系数法求得OM的中垂线的解析式,则R的坐标可利用m表示出来,然后利用勾股定理求得MR的长,则三角形的周长即可求得;
(3)作PM⊥x轴于点M,作PN⊥y轴于点N,证明△PNE≌△PMF,证得ME=MF,则OE+OF=OM+ON=
| 2 |
解答:解:(1)在y=-
x+3中,把y=x代入得x=-
x+3,
解得:x=2,
则A的坐标是(2,2);
(2)设M的横坐标是m,则M的坐标是(2m,2).
则OM的中点的坐标是(m,1),
设直线OM的解析式是y=kx,则2mk=2,解得:k=
,
则直线OM的解析式是y=
x,
设OM的中垂线的解析式是y=-mx+b,则-m2+b=1,
解得:b=m2+1.
则OM的中垂线的解析式是y=-mx+m2+1.
当y=0时,解得:x=
,则N的坐标是(
,0).
设直线MN的解析式是y=ax+c,
则
,
解得:
,
则直线MN的解析式是y=
x-
.
令x=2,则y=
.即R的坐标是(2,
).
则AR=2-
=
.
AM=2-m,
MR=
=
.
则△AMR的周长=
+(2-m)+
=4;
(3)证明:作PM⊥x轴于点M,作PN⊥y轴于点N.
则四边形OMNP是正方形,PM=PN=ON=OM=
OP,∠NPM=90°.
∵PE⊥PF,即∠EPF=90°,
∴∠NPE=∠MPF.
则在△PNE和△PMF中,
,
∴△PNE≌△PMF(ASA).
∴ME=MF,
则OE+OF=OM+ON=
OP.
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=2,
则A的坐标是(2,2);
(2)设M的横坐标是m,则M的坐标是(2m,2).
则OM的中点的坐标是(m,1),
设直线OM的解析式是y=kx,则2mk=2,解得:k=
| 1 |
| m |
则直线OM的解析式是y=
| 1 |
| m |
设OM的中垂线的解析式是y=-mx+b,则-m2+b=1,
解得:b=m2+1.
则OM的中垂线的解析式是y=-mx+m2+1.
当y=0时,解得:x=
| m2+1 |
| m |
| m2+1 |
| m |
设直线MN的解析式是y=ax+c,
则
|
解得:
|
则直线MN的解析式是y=
| 2m |
| m2-1 |
| 2(m2+1) |
| m2-1 |
令x=2,则y=
| 2-2m |
| m+1 |
| 2-2m |
| m+1 |
则AR=2-
| 2-2m |
| m+1 |
| 4m |
| m+1 |
AM=2-m,
MR=
(
|
| 2(m2+1) |
| m+1 |
则△AMR的周长=
| 4m |
| m+1 |
| 2(m2+1) |
| m+1 |

(3)证明:作PM⊥x轴于点M,作PN⊥y轴于点N.
则四边形OMNP是正方形,PM=PN=ON=OM=
| ||
| 2 |
∵PE⊥PF,即∠EPF=90°,
∴∠NPE=∠MPF.
则在△PNE和△PMF中,
|
∴△PNE≌△PMF(ASA).
∴ME=MF,
则OE+OF=OM+ON=
| 2 |
点评:本题考查了一次函数与三角形的全等的判定与性质,利用m表示出AR和MR的长是关键.

练习册系列答案
相关题目
 如图,已知O为△ABC内的一点,点D、E分别在边AB、AC上,且
如图,已知O为△ABC内的一点,点D、E分别在边AB、AC上,且 如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )
如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )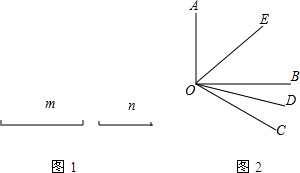 (1)尺规作图(不写作法,保留作图痕迹)已知:如图1,线段m,n.求作:线段AB=m+2n.
(1)尺规作图(不写作法,保留作图痕迹)已知:如图1,线段m,n.求作:线段AB=m+2n.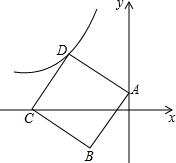 如图,正方形ABCD,A(0,1),C(-5,0),双曲线y=
如图,正方形ABCD,A(0,1),C(-5,0),双曲线y=