题目内容
 如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )
如图,∠AOB=∠COD,若∠AOD=110°,∠BOC=70°,则以下结论正确的个数为( )①∠AOC=∠BOD=90°;②∠AOB=20°;③∠AOB=∠AOD-∠AOC;④∠AOB=
| 2 |
| 11 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:角的计算
专题:
分析:根据已知条件和图形可以得到:∠AOD=∠BOC+2∠COD=110°,则∠AOB=∠COD=20°,由此可以对以下选项通过计算可以做出正确的判定.
解答: 解:如图,∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,
解:如图,∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,
∴∠AOD=∠BOC+2∠COD=70°+2∠COD=110°,则∠AOB=∠COD=20°.
①∵∠AOB=∠COD,
∴∠BOC+∠AOB=∠BOC+∠COD=90°,即∠AOC=∠BOD=90°,故①正确;
②∠AOB=∠COD=20°.故②正确;
③由①知,∠AOC=∠BOD=90°,
∴∠AOB=∠AOD-∠BOD=∠AOD-∠AOC,
故③正确;
④∵∠AOB=20°,∠BOD=90°,
∴∠AOB=
∠BOD.
故④错误.
综上所述,正确的结论有3个.
故选:C.
 解:如图,∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,
解:如图,∵∠AOB=∠COD,∠AOD=110°,∠BOC=70°,∴∠AOD=∠BOC+2∠COD=70°+2∠COD=110°,则∠AOB=∠COD=20°.
①∵∠AOB=∠COD,
∴∠BOC+∠AOB=∠BOC+∠COD=90°,即∠AOC=∠BOD=90°,故①正确;
②∠AOB=∠COD=20°.故②正确;
③由①知,∠AOC=∠BOD=90°,
∴∠AOB=∠AOD-∠BOD=∠AOD-∠AOC,
故③正确;
④∵∠AOB=20°,∠BOD=90°,
∴∠AOB=
| 2 |
| 9 |
故④错误.
综上所述,正确的结论有3个.
故选:C.
点评:本题考查了角的计算.解题时利用了“数形结合”的数学思想.

练习册系列答案
相关题目
在△ABC中,∠C=90°,AC=3,AB=5,则sinA的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在平面直角坐标系xOy中,点A(-m,0)和点B(0,2m)(m>0),点C在x轴上(不与点A重合)
如图,在平面直角坐标系xOy中,点A(-m,0)和点B(0,2m)(m>0),点C在x轴上(不与点A重合)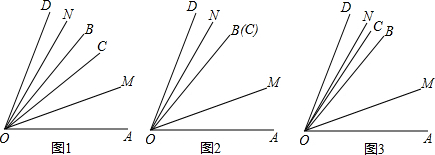
 如图,OC平分∠AOD,且∠2:∠3:∠4=1:2:4,求∠1的度数.
如图,OC平分∠AOD,且∠2:∠3:∠4=1:2:4,求∠1的度数.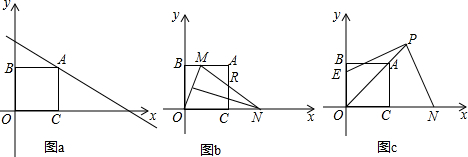
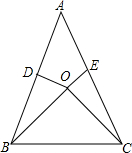 (1)如图,点O是△ABC内一点,OD⊥AB于D,OE⊥AC于E,且OB=OC,OD=OE,求证:△ABC是等腰三角形.
(1)如图,点O是△ABC内一点,OD⊥AB于D,OE⊥AC于E,且OB=OC,OD=OE,求证:△ABC是等腰三角形.