题目内容
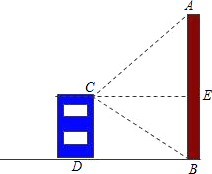在旧城改造中，要拆除一烟囱AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45°，到B点的俯角为30°，问离B点30米远的保护文物是否在危险区内？（| 3 |
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：首先分析图形：根据题意构造直角三角形；本题涉及多个直角三角形，应利用其公共边构造等量关系，进而可求出答案．
解答：答：文物在危险区内．
解：在Rt△AEC中，∠ACE=45°，
则CE=EA，
∵DB=CE=21m，
∴DB=EA=21m，
在Rt△CEB中，∠BCE=30°，
则tan30°=
，即BE=ECtan30°，
∴BE=21×
=7
m，
∴AB=AE+EB=（21+7
）m，
∵AB=（21+7
）＞30，
∴文物在危险区内．
解：在Rt△AEC中，∠ACE=45°，
则CE=EA，
∵DB=CE=21m，
∴DB=EA=21m，
在Rt△CEB中，∠BCE=30°，
则tan30°=
| BE |
| EC |
∴BE=21×
| ||
| 3 |
| 3 |
∴AB=AE+EB=（21+7
| 3 |
∵AB=（21+7
| 3 |
∴文物在危险区内．
点评：本题考查了解直角三角形的应用--仰角俯角，要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
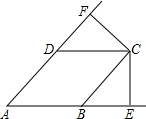如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，
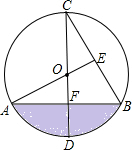如图，CD为⊙O的直径，CD⊥AB于点F，AO⊥BC于点E，AO=2．
如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．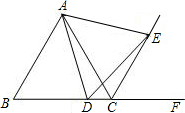
如图，△ABC为等边三角形，D为BC边上一点，以AD为边作∠ADE=60°，DE与△ABC的外角平分线CE交于点E，连接AE，且CE=BD．求证：△ADE是等边三角形．
已知有理数a、b在数轴上的位置如图所示，化简：|a+b|+|a|-（-b）+|ab|．
已知：如图，在△ABC中，∠C=90°，sinA=