题目内容
求一个正数的算术平方根，有些数可以直接可得，如
；有些数则不能直接求得，如
，除通过计算器可以求得．还可以通过一组数的内在联系，运用规律求得，观察下表：
（1）根据表中的规律，可以求得：
= ，
= ；
（2）根据表中的规律，还可以由
=1.435，求得：
= ，
= ，
= ．
| 4 |
| 5 |
| n | 0.09 | 9 | 900 | 90000 | … | ||
|
0.3 | 3 | 30 | 300 | … |
| 0.0009 |
| 9000000 |
（2）根据表中的规律，还可以由
| 2.06 |
| 0.0206 |
| 20600 |
| 8.24 |
考点：算术平方根
专题：规律型
分析：（1）从被开方数和算术平方根的小数点的移动位数考虑解答；
（2）根据（1）中的规律解答即可．
（2）根据（1）中的规律解答即可．
解答：解：观察表格得：被开方数扩大或缩小102n倍，非负数的算术平方根就相应的扩大或缩小10n倍；
或者说成被开方数的小数点向左或向右移动2n位，算术平方根的小数点就向左或向右移动n位；
故（1）
=0.03，
=3000；
（2）由
=1.435，得：
=0.1435，
=143.5，
=2×1.435=2.87．
故答案为：0.03，3000，0.1435，143.5，2.87：
或者说成被开方数的小数点向左或向右移动2n位，算术平方根的小数点就向左或向右移动n位；
故（1）
| 0.0009 |
| 9000000 |
（2）由
| 2.06 |
| 0.0206 |
| 20600 |
| 8.24 |
故答案为：0.03，3000，0.1435，143.5，2.87：
点评：本题考查了算术平方根，解题的关键在于从小数点的移动位数考虑．
练习册系列答案
相关题目
如图，梯形ABCD中，AD∥BC，设AC，BD交于O点，则图中共有对面积相等的三角形（ ）| A、2 | B、3 | C、4 | D、5 |
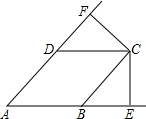如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，
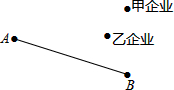在国家“西电东送”工程中，为发展地方经济，促进甲、乙两大型企业发展，又为方便A，B两村群众，在如图所示的地理位置中，准备修一个变电站P，使变电站到A，B两村的距离相等，又要到甲、乙两企业的距离最短，请在图中作出P点的位置．（保留作图痕迹）
画出函数y=-2x+2的图象，观察图象并回答下列问题．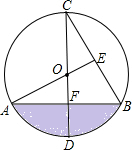
如图，CD为⊙O的直径，CD⊥AB于点F，AO⊥BC于点E，AO=2．
如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．