题目内容
当-2<x<2时,下列函数:①y=2x;②y=-2+
x;③y=-
;④y=x2+6x+8,函数值y随自变量x增大而增大的有( )
| 1 |
| 3 |
| 6 |
| x |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
考点:二次函数的性质,一次函数的性质,正比例函数的性质,反比例函数的性质
专题:
分析:根据一次函数,反比例函数,二次函数的增减性,逐一判断.
解答:解::①y=2x中k>0,故y随自变量x增大而增大,满足题意;
②y=-2+
xk>0,故y随自变量x增大而增大,满足题意;
③y=-
中在每一个象限y随自变量x增大而增大,不满足题意;
④y=x2+6x+8,对称轴为x=-3,当x>-3时,y随自变量x增大而增大,故满足题意,
故选C.
②y=-2+
| 1 |
| 3 |
③y=-
| 6 |
| x |
④y=x2+6x+8,对称轴为x=-3,当x>-3时,y随自变量x增大而增大,故满足题意,
故选C.
点评:本题综合考查二次函数、一次函数、反比例函数、正比例函数的增减性(单调性),是一道难度中等的题目.

练习册系列答案
相关题目
m与n两数的倒数的和是( )
A、m+
| ||||
B、
| ||||
C、
| ||||
D、
|
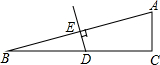 如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=( )
如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=( )| A、5 | B、10 | C、15 | D、20 |
 如图,梯形ABCD中,AD∥BC,设AC,BD交于O点,则图中共有对面积相等的三角形( )
如图,梯形ABCD中,AD∥BC,设AC,BD交于O点,则图中共有对面积相等的三角形( )| A、2 | B、3 | C、4 | D、5 |
下列运算正确的是( )
| A、(a2)3÷a4=a | ||||
B、x2÷x•
| ||||
| C、(6x2+3x)÷3x=2x | ||||
D、(-
|
 如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°.求证:以MN,BN,AM为边的三角形是直角三角形.
如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°.求证:以MN,BN,AM为边的三角形是直角三角形.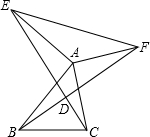 已知:AB=AE,AB⊥AE,AC=AF,AC⊥AF.
已知:AB=AE,AB⊥AE,AC=AF,AC⊥AF.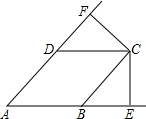 如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,
如图,四边形ABCD是菱形,CE⊥AB交AB延长线于E,CF⊥AD交AD延长线于F,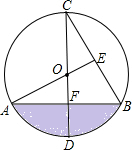 如图,CD为⊙O的直径,CD⊥AB于点F,AO⊥BC于点E,AO=2.
如图,CD为⊙O的直径,CD⊥AB于点F,AO⊥BC于点E,AO=2.