题目内容
16.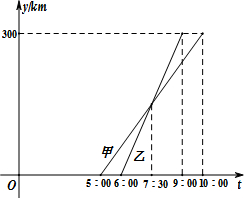 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
分析 由图示知:A,B两城相距300km,甲车从5:00出发,乙车从6:00出发;甲车10:00到达B城,乙车9:00到达B城;计算出乙车的平均速度为:300÷(9-6)=100(km/h),当乙车7:30时,乙车离A的距离为:100×1.5=150(km),得到点A(7.5,150)点B(5,0),设甲的函数解析式为:y=kt+b,把点A(7.5,150),B(5,0)代入解析式,求出甲的解析式,当t=9时,y=60×9-300=240,所以9点时,甲距离开A的距离为240km,则当乙车到达B城时,甲车离B城的距离为:300-240=60km.
解答 解:如图,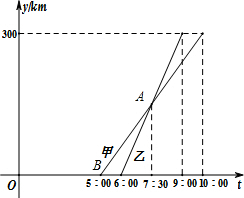
由图示知:A,B两城相距300km,甲车从5:00出发,乙车从6:00出发;甲车10:00到达B城,乙车9:00到达B城;
乙车的平均速度为:300÷(9-6)=100(km/h),
当乙车7:30时,乙车离A的距离为:100×1.5=150(km),
∴点A(7.5,150)
由图可知点B(5,0)
设甲的函数解析式为:y=kt+b,
把点A(7.5,150),B(5,0)代入y=kt+b得:$\left\{\begin{array}{l}{7.5t+b=150}\\{5t+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=60}\\{t=-300}\end{array}\right.$,
∴甲的函数解析式为:y=60t-300,
当t=9时,y=60×9-300=240,
∴9点时,甲距离开A的距离为240km,
∴则当乙车到达B城时,甲车离B城的距离为:300-240=60km.
故答案为:60.
点评 本题考查了一次函数的应用,解决本题的关键是求甲的函数解析式,即可解答.

| A. | AD=BC | B. | AC=BD | C. | ∠A=∠C | D. | ∠A=∠B |
 如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
 在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.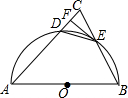 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.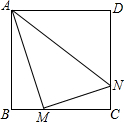 如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.
如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.