题目内容
1.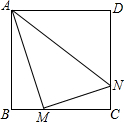 如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.
如图,正方形ABCD的边长为8,M、N分别是边BC、CD上的两个动点,当M点在BC上运动时,始终保持AM和MN垂直.(1)证明:Rt△ABM∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,梯形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时,Rt△ABM∽Rt△AMN?
分析 (1)由四边形ABCD为正方形,得到一对直角相等,再由AM垂直于MN,得到∠AMN为直角,利用同角的余角相等得到一对角相等,利用两对角相等的三角形相似即可得证;
(2)由(1)得出的相似三角形,可得对应边成比例,根据BM=x与AB=8,表示出CN,由CN为上底,AB为下底,BC为高,利用梯形的面积公式列出y与x的函数关系式,利用二次函数的性质确定出梯形ABCN面积最大时M的位置,并求出最大面积即可;
(3)由一对直角相等,要使Rt△ABM∽Rt△AMN,必须有$\frac{AB}{AM}$=$\frac{BM}{MN}$,表示出BM,由(1)的结论表示出CM,可得出BM=CM,即此时M为BC的中点.
解答 (1)证明:在正方形ABCD中,∠B=∠C=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠CMN+∠AMB=90°.
在Rt△ABM中,∠BAM+∠AMB=90°,
∴∠BAM=∠CMN,
∴Rt△ABM∽Rt△MCN;
(2)∵Rt△ABM∽Rt△MCN,BM=x,
∴$\frac{AB}{MC}$=$\frac{BM}{CN}$,即$\frac{8}{8-x}$=$\frac{x}{CN}$,
整理得:CN=$\frac{-{x}^{2}+8x}{8}$,
∴y=S梯形ABCN=$\frac{1}{2}$×($\frac{-{x}^{2}+8x}{8}$+8)×8=-$\frac{1}{2}$x2+4x+32=-$\frac{1}{2}$(x-4)2+40(0<x<8),
则当x=4,即M点运动到BC的中点时,梯形ABCN的面积最大,最大值为40;
(3)∵∠B=∠AMN=90°,
∴要使Rt△ABM∽Rt△AMN,必须有$\frac{AB}{AM}$=$\frac{BM}{MN}$,即BM=$\frac{AB•MN}{AM}$,
由(1)知$\frac{AM}{MN}$=$\frac{AB}{MC}$,即MC=$\frac{AB•MN}{AM}$,
∴BM=MC,
则当点M运动到BC的中点时,Rt△ABM∽Rt△MCN.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,二次函数的性质,梯形的面积求法,以及正方形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\frac{3}{2}$$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
| A. | 中位数 | B. | 方差 | C. | 众数 | D. | 平均数 |
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
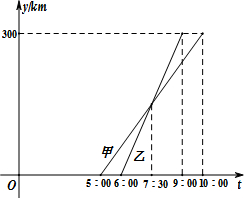 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.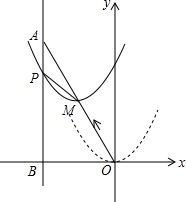 如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知点A坐标为(-2,4),直线x=-2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到A点时停止移动.
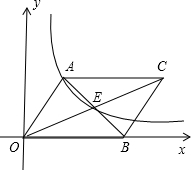 如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.
如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.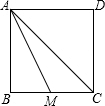 如图,正方形ABCD中,点M是边BC上的中点,联结AM,AC,则sin∠MAC=$\frac{\sqrt{10}}{5}$.
如图,正方形ABCD中,点M是边BC上的中点,联结AM,AC,则sin∠MAC=$\frac{\sqrt{10}}{5}$.