题目内容
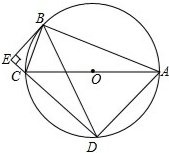 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E. (1)求证:∠BCA=∠BAD;
(2)若∠BAC=30°,求DE的长;
(3)求证:BE是⊙O的切线.
考点:切线的判定
专题:证明题
分析:(1)根据等腰三角形的性质,由BD=BA得到∠BDA=∠BAD,再根据圆周角定理得到∠BCA=∠BDA,所以∠BCA=∠BAD;
(2)在Rt△ABC中,根据含30度的直角三角形三边的关系得到AB=
BC=5
,则BD=5
,在Rt△BED中,利用∠BDC=∠BAC=30°,则可计算出BE=
BD=
,DE=
BE=
;
(3)连结BO并延长交AD于F,如图,根据等腰三角形的性质和外心的性质得到BF⊥AD,再利用圆内接四边形的性质得∠ADC=180°-∠ABC=90°,所以BF∥DE,而BE⊥DE,于是得到BE⊥BF,然后根据切线得判定定理即可得到BE是⊙O的切线.
(2)在Rt△ABC中,根据含30度的直角三角形三边的关系得到AB=
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
5
| ||
| 2 |
| 3 |
| 15 |
| 2 |
(3)连结BO并延长交AD于F,如图,根据等腰三角形的性质和外心的性质得到BF⊥AD,再利用圆内接四边形的性质得∠ADC=180°-∠ABC=90°,所以BF∥DE,而BE⊥DE,于是得到BE⊥BF,然后根据切线得判定定理即可得到BE是⊙O的切线.
解答:(1)证明:∵BD=BA,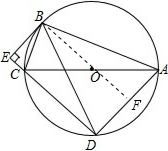
∴∠BDA=∠BAD,
∵∠BCA=∠BDA,
∴∠BCA=∠BAD;
(2)解:在Rt△ABC中,∵∠BAC=30°,BC=5,
∴AB=
BC=5
,
∴BD=BA=5
,
∵BE⊥DC,
∴∠BED=90°,
而∠BDC=∠BAC=30°,
∴BE=
BD=
,
∴DE=
BE=
;
(3)证明:连结BO并延长交AD于F,如图,
∵BA=BD,
∴BF⊥AD,
∵∠ADC=180°-∠ABC=90°,
∴BF∥DE,
而BE⊥DE,
∴BE⊥BF,
∴BE是⊙O的切线.

∴∠BDA=∠BAD,
∵∠BCA=∠BDA,
∴∠BCA=∠BAD;
(2)解:在Rt△ABC中,∵∠BAC=30°,BC=5,
∴AB=
| 3 |
| 3 |
∴BD=BA=5
| 3 |
∵BE⊥DC,
∴∠BED=90°,
而∠BDC=∠BAC=30°,
∴BE=
| 1 |
| 2 |
5
| ||
| 2 |
∴DE=
| 3 |
| 15 |
| 2 |
(3)证明:连结BO并延长交AD于F,如图,
∵BA=BD,
∴BF⊥AD,
∵∠ADC=180°-∠ABC=90°,
∴BF∥DE,
而BE⊥DE,
∴BE⊥BF,
∴BE是⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题:
华夏古诗词源远流长,有许多古诗词与勾股定理有紧密联系,下面是明朝大数学家程大位所著的《直指算法统宗》里的一道题: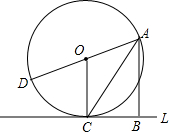 如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形?
如图所示,直线L切⊙O于点C,AD为⊙O的任意一条直径,点B在直线L上,且∠BAC=∠CAD(AD与AB不在一条直线上),试判断四边形ABCO为怎样的特殊四边形?