题目内容
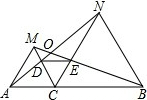 如图所示,已知点C为线段AB上的一点,△ACM、△BCN都是等边三角形,连接DE.
如图所示,已知点C为线段AB上的一点,△ACM、△BCN都是等边三角形,连接DE.(1)试探究AN与BM的关系;
(2)求证:AD=ME;
(3)连接OC,证明∠AOC为60°.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:证明题
分析:(1)由△ACM、△BCN都是等边三角形可以得到△ACN与△MCB全等的条件,进而得到结论;
(2)由△ACN≌△MCB就可以得出∠CMB=∠CAN,再证明△MCE≌△ACD就可以得出结论;
(3)过C作CZ⊥AN于Z,作CF⊥BM于F,求出∠AOB=120°,根据面积公式求出CZ=CF,推出OC平分∠AOB,即可得出答案.
(2)由△ACN≌△MCB就可以得出∠CMB=∠CAN,再证明△MCE≌△ACD就可以得出结论;
(3)过C作CZ⊥AN于Z,作CF⊥BM于F,求出∠AOB=120°,根据面积公式求出CZ=CF,推出OC平分∠AOB,即可得出答案.
解答:(1)解:AN=BM,理由如下:
∵△ACM、△BCN都是等边三角形,
∴AC=MC,∠ACM=∠BCN,NC=BC,
∴∠ACN=∠MCB,
在△ACN与△MCB中,
,
∴△ACN≌△MCB
∴AN=BM;
(2)证明:∵△ACN≌△MCB,
∴∠CAN=∠CMB,
∵△ACM、△BCN都是等边三角形.
∴∠ACM=∠NCB=60°
∵∠ACM+∠NCB+∠MCN=180°,
∴∠MCN=60°.
∴∠ACM=∠MCN.
在△CAD和△CEM中,
,
∴△CAD≌△CEM(SAS),
∴AD=ME;
(3)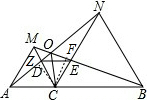
证明:∵△ACN≌△MCB,
∴∠ANC=∠MBC,
∴∠AOM=∠MBC+∠NAC=∠ANC+∠NAC=∠NCB=60°,
∴∠AOB=180°-60°=120°,
过C作CZ⊥AN于Z,作CF⊥BM于F,
∵△ACN≌△MCB,
∴AN=BM,S△ACN=S△MCB,
∴
AN×CZ=
BM×CF,
∴CZ=CF,
∴OC平分∠AOB,
∴∠AOC=60°.
∵△ACM、△BCN都是等边三角形,
∴AC=MC,∠ACM=∠BCN,NC=BC,
∴∠ACN=∠MCB,
在△ACN与△MCB中,
|
∴△ACN≌△MCB
∴AN=BM;
(2)证明:∵△ACN≌△MCB,
∴∠CAN=∠CMB,
∵△ACM、△BCN都是等边三角形.
∴∠ACM=∠NCB=60°
∵∠ACM+∠NCB+∠MCN=180°,
∴∠MCN=60°.
∴∠ACM=∠MCN.
在△CAD和△CEM中,
|
∴△CAD≌△CEM(SAS),
∴AD=ME;
(3)

证明:∵△ACN≌△MCB,
∴∠ANC=∠MBC,
∴∠AOM=∠MBC+∠NAC=∠ANC+∠NAC=∠NCB=60°,
∴∠AOB=180°-60°=120°,
过C作CZ⊥AN于Z,作CF⊥BM于F,
∵△ACN≌△MCB,
∴AN=BM,S△ACN=S△MCB,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴CZ=CF,
∴OC平分∠AOB,
∴∠AOC=60°.
点评:本题考查了等边三角形的性质和判定,角平分线性质,全等三角形的性质和判定的应用,题目综合性比较强,有一定的难度.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
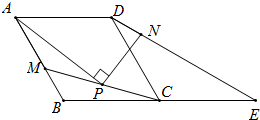 已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.
已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.