题目内容
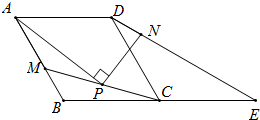 已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.
已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.(1)探究PA与PN的关系,并证明你的结论.
(2)探究DN与AM的关系,并证明你的结论.
考点:菱形的性质
专题:
分析:(1)先证△MGP≌△CPI,再得出△JPG≌△NPI,最后证明△AGN是等边三角形,即可求解;
(2)首先证明A、H、N、P四点共圆,则∠AHN=90°,然后利用三角函数即可求解.
(2)首先证明A、H、N、P四点共圆,则∠AHN=90°,然后利用三角函数即可求解.
解答: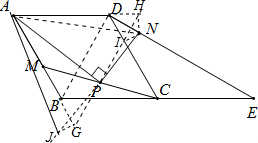 解:(1)连接BD.
解:(1)连接BD.
过点P作HG∥BD交AD、AB延长线于点H、G.延长NO到J使IP=NP,连接AN、AJ.
∵P是MC的中点,MG∥IC
∴△MGP≌△CIP,
∴PI=PG,
∴△JPG≌△NPI,
∴JG=NI.
∵菱形ABCD中,∠BAD=180°-∠ABC=60°,AD=AB,
∴△ABD是等边三角形.
又∵HG∥BD,
∴△DIH和△AGH都是等边三角形.
∴△NHD≌△NID,
∴NI=NH=JG.
∵P是MC的中点,AP⊥NJ,
∴JG=AN.
在△AJG和△ANH中,
,
∴△AJG≌△ANH(SSS).
又∵△AJN是等边三角形,
∴PA=
PN;
(2)设AM=x,DI=y,AB=a,
则CI=MG=a-y,
∵四边DBGI是平行四边形,
∴BG=y,
∴MB=a-y-y,
∵x+MB=a,
∴x+a-y-y=a,
∴x=2y,
∴AM=2DI.
∵∠AHP=∠ANP=60°,
∴A、H、N、P四点共圆.
∵∠APN=90°,
∴∠AHN=90°,则y=
DN,
∴DI=
DN.
∴AM=
DN.
 解:(1)连接BD.
解:(1)连接BD.过点P作HG∥BD交AD、AB延长线于点H、G.延长NO到J使IP=NP,连接AN、AJ.
∵P是MC的中点,MG∥IC
∴△MGP≌△CIP,
∴PI=PG,
∴△JPG≌△NPI,
∴JG=NI.
∵菱形ABCD中,∠BAD=180°-∠ABC=60°,AD=AB,
∴△ABD是等边三角形.
又∵HG∥BD,
∴△DIH和△AGH都是等边三角形.
∴△NHD≌△NID,
∴NI=NH=JG.
∵P是MC的中点,AP⊥NJ,
∴JG=AN.
在△AJG和△ANH中,
|
∴△AJG≌△ANH(SSS).
又∵△AJN是等边三角形,
∴PA=
| 3 |
(2)设AM=x,DI=y,AB=a,
则CI=MG=a-y,
∵四边DBGI是平行四边形,
∴BG=y,
∴MB=a-y-y,
∵x+MB=a,
∴x+a-y-y=a,
∴x=2y,
∴AM=2DI.
∵∠AHP=∠ANP=60°,
∴A、H、N、P四点共圆.
∵∠APN=90°,
∴∠AHN=90°,则y=
| ||
| 2 |
∴DI=
| ||
| 2 |
∴AM=
| 3 |
点评:本题是推理证明题,主要考查菱形的边的性质,同时综合利用全等三角形的判定方法及等腰三角形的性质,正确作出辅助线是关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图所示,以Rt△ABC的三条边为直径分别向外作半圆,设以BC为直径的半圆的面积记作S1,以AC为直径的半圆的面积记作S2,以AB为直径的半圆的面积记作S3,则S1、S2、S3之间的关系正确的是( )
如图所示,以Rt△ABC的三条边为直径分别向外作半圆,设以BC为直径的半圆的面积记作S1,以AC为直径的半圆的面积记作S2,以AB为直径的半圆的面积记作S3,则S1、S2、S3之间的关系正确的是( )| A、S1+S2>S3 |
| B、S1+S2<S3 |
| C、S1+S2=S3 |
| D、无法确定 |
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A、若AB∥CD,则∠3=∠4 |
| B、若AD∥BC,则∠3=∠4 |
| C、若∠1=∠2,则AB∥CD |
| D、若∠3=∠4,则AD∥BC |
 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=
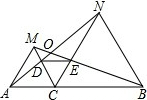 如图所示,已知点C为线段AB上的一点,△ACM、△BCN都是等边三角形,连接DE.
如图所示,已知点C为线段AB上的一点,△ACM、△BCN都是等边三角形,连接DE.