题目内容
甲、乙两船航行于海上，甲船的位置在乙船北方125km处，以15km/h的速度向东行驶，乙船以20km/h的速度向北行驶，则多久两船相距最近？最近距离为多少？
考点：勾股定理的应用,二次函数的最值
专题：
分析：根据题意画出图形，进而利用勾股定理求出S=
，进而求出最值即可．
| (15x)2+(125-20x)2 |
解答：
解：如图所示：设x小时后两船相距S，
根据题意可得：OA=（125-20x）km，OB=15km
则S=
=
=
=
所以当x=4时，两船相距最近为75km．
解：如图所示：设x小时后两船相距S，根据题意可得：OA=（125-20x）km，OB=15km
则S=
| (15x)2+(125-20x)2 |
=
| 625x2-5000x+15625 |
=
| 625(x2-8x)+15625 |
=
| 625(x-4)2+5625 |
所以当x=4时，两船相距最近为75km．
点评：此题主要考查了勾股定理的应用以及二次函数最值求法，得出S与x的函数关系式是解题关键．
练习册系列答案
相关题目
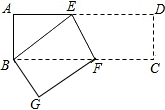如图，长方形ABCD中，折痕为EF，将此长方形沿EF折叠，使点B与D重合，已知AB=3cm，AD=9cm．
如图，在平面直角坐标系中，直线y=
如图，在△ABC中，AD是边BC上的高，BC=AD=8，sinB=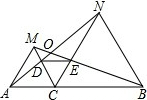
如图所示，已知点C为线段AB上的一点，△ACM、△BCN都是等边三角形，连接DE．
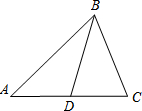已知等腰△ABC中，AB=AC，D为AC的中点，且BD把△ABC的周长分成12和14两部分，求△ABC各边的长．