题目内容
若点P为△ABC外心，已知∠A=100°，则∠BPC的度数为 ．
考点：三角形的外接圆与外心
专题：
分析：作圆周角BDC，根据圆内接四边形的性质求出∠D，根据圆周角定理得出∠BPC=2∠D，代入求出即可．
解答：
解：如图，作圆周角BDC，
∵四边形ABDC是圆内接四边形，∠A=100°，
∴∠D=180°-∠A=80°，
∴∠BPC=2∠BDC=160°，
故答案为：160°．
解：如图，作圆周角BDC，
∵四边形ABDC是圆内接四边形，∠A=100°，
∴∠D=180°-∠A=80°，
∴∠BPC=2∠BDC=160°，
故答案为：160°．
点评：本题考查了圆内接四边形的性质，圆周角定理的应用，注意：圆内接四边形的对角互补．
练习册系列答案
相关题目
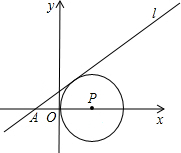如图，点P在x轴上，OP=2，以点P为圆心，OP长为半径作圆，已知经过点A（-2，0）的直线l的函数解析式为y=kx+b，当l分别与⊙P相交、相切、相离时，求b的取值范围．
如图，在平面直角坐标系中，直线y=
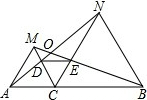如图所示，已知点C为线段AB上的一点，△ACM、△BCN都是等边三角形，连接DE．
如图所示，以Rt△ABC的三条边为直径分别向外作半圆，设以BC为直径的半圆的面积记作S1，以AC为直径的半圆的面积记作S2，以AB为直径的半圆的面积记作S3，则S1、S2、S3之间的关系正确的是（ ）| A、S1+S2＞S3 |
| B、S1+S2＜S3 |
| C、S1+S2=S3 |
| D、无法确定 |
已知一个Rt△的两直角边长分别为3和4，则斜边的平方是（ ）
| A、25 | B、14 | C、7 | D、5 |