题目内容
9.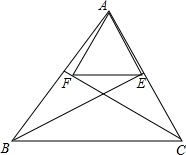 如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.
如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.
分析 延长AF、AE分别交BC于M、N,证明△CFA≌△CFM得AF=FM,同理AE=EN,根据三角形中位线定理即可证明.
解答  证明:延长AF、AE分别交BC于M、N.
证明:延长AF、AE分别交BC于M、N.
在△CFA和△CFM中,
$\left\{\begin{array}{l}{∠FCA=∠FCM}\\{CF=CF}\\{∠CFA=∠CFM=90°}\end{array}\right.$,
∴△CFA≌△CFM,
∴AF=FM,同理可证:AE=EN,
∴EF∥MN,即EF∥BC.
点评 本题考查全等三角形的判定和性质、角平分线的定义、三角形中位线定理,解题的关键是辅助线的添加,属于中考常考题型.

练习册系列答案
相关题目
19.计算3x4÷x2=( )
| A. | 3x2 | B. | 2x2 | C. | x2 | D. | 3x6 |
4.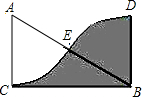 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
 已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?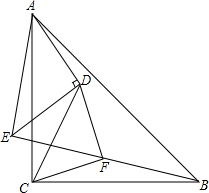 如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.