题目内容
8.解下列方程或不等式组,并把不等式的解集表示在数轴上.(1)$\frac{x+2}{4}-\frac{2x-1}{6}=1$
(2)$\left\{\begin{array}{l}3(x+2)>x+4\\ \frac{x}{3}≤\frac{x+1}{4}\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)先求出不等式的解集,再求出不等式组的解集,最后表示出来即可.
解答 解:(1)去分母得:3(x+2)-2(2x-1)=12,
3x+6-4x+2=12
3x-4x=12-2-6
-x=4
x=-4;
(2)$\left\{\begin{array}{l}{3(x+2)>x+4①}\\{\frac{x}{3}≤\frac{x+1}{4}②}\end{array}\right.$
∵解不等式①得:x>-1,
解不等式②得:x≤3,
∴不等式组的解集为-1<x≤3,
在数轴上表示为: .
.
点评 本题考查了解一元一次方程和解一元一次不等式组在数轴上表示不等式组的解集的应用,能正确根据等式的性质解方程是解(1)的关键,能求出不等式组的解集是解(2)的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图所示,矩形ABCD中,AB=3,AD=2,点M在CD上,若AM平分∠DMB,则DM的长是( )
如图所示,矩形ABCD中,AB=3,AD=2,点M在CD上,若AM平分∠DMB,则DM的长是( )
 如图所示,矩形ABCD中,AB=3,AD=2,点M在CD上,若AM平分∠DMB,则DM的长是( )
如图所示,矩形ABCD中,AB=3,AD=2,点M在CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{5}-\frac{3}{2}$ | D. | 3-$\sqrt{5}$ |
17.下列各式中,不能用平方差公式计算的是( )
| A. | (-x+y)(x-y) | B. | (x2-2y2)(x2+2y2) | C. | (x+y-z)(-z-y+x) | D. | (2x-y)(-y-2x) |
 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2). 如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).
如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).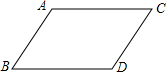 如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm.
如图,将长为4cm的线段AB沿着点A到点C的方向平移6cm得到线段CD,那么四边形ABDC的周长是20cm. 如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3,4、5、6、7、8,任意转动转盘一次,当转盘停止转动时,对于下列事件:
如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3,4、5、6、7、8,任意转动转盘一次,当转盘停止转动时,对于下列事件: