题目内容
9.在含有30°的角的直角三角形中,较短的直角边与斜边的比是$\frac{1}{2}$,较长的直角边与较短的直角边的比是$\sqrt{3}$,斜边上的中线与斜边的比是$\frac{1}{2}$.分析 根据含30度角的直角三角形的性质即可作答.
解答  解:如图,∵∠A=30°,∠ACB=90°,
解:如图,∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∴$\frac{BC}{AB}$=sinA=sin30°=$\frac{1}{2}$,
$\frac{AC}{BC}$=tanB=tan60°=$\sqrt{3}$,
∵BD=$\frac{1}{2}$AB=BC,
∴△BCDs是等边三角形,
∴CD=BD=$\frac{1}{2}$AB,
∴$\frac{CD}{AB}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$,$\sqrt{3}$,$\frac{1}{2}$.
点评 本题考查了含30度角的直角三角形的性质,熟记在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
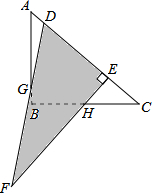 一副三角尺按如图所示方式放置,试求∠AGF的度数.
一副三角尺按如图所示方式放置,试求∠AGF的度数.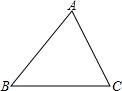 如图,在△ABC中,画出它们的三条中线AD、BE、CF,三条中线交于一点G,AG与GD的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立?
如图,在△ABC中,画出它们的三条中线AD、BE、CF,三条中线交于一点G,AG与GD的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立?