题目内容
2．已知：①平行四边形 ②矩形 ③菱形 ④等腰三角形 ⑤等腰梯形．这5种图形中，既是中心对称图形，又是轴对称图形的有（ ）| A． | 2种 | B． | 3种 | C． | 4种 | D． | 5种 |
分析 根据中心对称图形和轴对称图形的概念对各图形分析判断即可得解．
解答 解：①平行四边形，是中心对称图形，不是轴对称图形；
②矩形，既是中心对称图形，又是轴对称图形；
③菱形，既是中心对称图形，又是轴对称图形；
④等腰三角形，不是中心对称图形，是轴对称图形；
⑤等腰梯形，不是中心对称图形，是轴对称图形；
综上所述，既是中心对称图形，又是轴对称图形的有矩形和菱形共2种．
故选A．
点评 本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
如图，已知∠1+∠2=180°，∠B=∠3，试判断∠BAC和∠CED的大小关系，并说明理由．
10．下面各条件中，能判定四边形是平行四边形的是（ ）
| A． | 对角线互相垂直 | B． | 两组对边分别相等 | ||
| C． | 一组对角相等 | D． | 一组对边相等，另一组对边平行 |
17．若关于x的不等式（a-2）x＜2-a的解集是x＞-1，则a的取值范围是（ ）
| A． | a＞0 | B． | a＞2 | C． | a＜0 | D． | a＜2 |
7．
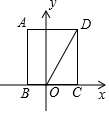如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2$\sqrt{3}$，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是（ ）
如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2$\sqrt{3}$，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是（ ）| A． | （-$\sqrt{3}$，1） | B． | （-1，$\sqrt{3}$） | C． | （-1，$\sqrt{3}$）或（1，-$\sqrt{3}$） | D． | （-$\sqrt{3}$，1）或（1，-$\sqrt{3}$） |
如图，水平桌面上有个内部装水的长方体箱子，箱内有一个与底面垂直的隔板，且隔板左右两侧的水面高度为别为40公分，50公分，今将隔板抽出，若过程中箱内的水量未改变，且不计箱子及隔板厚度，则根据图中的数据，求隔板抽出后水面静止时，箱内的水面高度为多少公分（ ）