题目内容
(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成 个三角形.若是一个六边形,可以分割成 个三角形.n边形可以分割成 个三角形.

(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?

(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?
考点:规律型:图形的变化类
专题:
分析:(1)从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n-2)个三角形,依此作答;
(2)多边形内一点,可与多边形顶点连接n条线段,构造出n个三角形;
(3)若P点取在一边上,则可以与其他顶点连接出n-2条线段,可以分n边形为(n-1)个三角形.
(2)多边形内一点,可与多边形顶点连接n条线段,构造出n个三角形;
(3)若P点取在一边上,则可以与其他顶点连接出n-2条线段,可以分n边形为(n-1)个三角形.
解答:解:(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成5-2=3个三角形.
若是一个六边形,可以分割成6-2=4个三角形,n边形可以分割成(n-2)个三角形.
故答案为:3,4,(n-2);
(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成n个三角形;
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成n-1个三角形.
若是一个六边形,可以分割成6-2=4个三角形,n边形可以分割成(n-2)个三角形.
故答案为:3,4,(n-2);
(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成n个三角形;
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成n-1个三角形.
点评:本题主要考查了多边形的性质,找出该点在不同状态下的规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,是由5个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
如图,是由5个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
| 3 | 8 |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、±2
|
 如图,A、B两点是正方体上的两个顶点,在这个平面展开图中的距离为6,则这两点在正方体上的距离为
如图,A、B两点是正方体上的两个顶点,在这个平面展开图中的距离为6,则这两点在正方体上的距离为 正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积
正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积
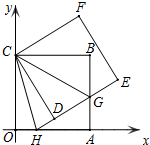 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.