题目内容
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利过程.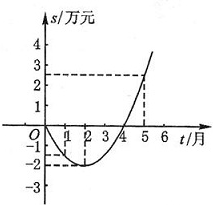 下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
 下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
考点:二次函数的应用
专题:
分析:(1)本题是通过构建函数模型解答销售利润的问题,应根据图象以及题目中所给的信息来列出S与t之间的函数关系式;
(2)把S=30代入累计利润S=
t2-2t的函数关系式里,求得月份;
(3)分别t=7,t=8,代入函数解析S=
t2-2t,再把总利润相减就可得出.
(2)把S=30代入累计利润S=
| 1 |
| 2 |
(3)分别t=7,t=8,代入函数解析S=
| 1 |
| 2 |
解答:解:(1)由图象可知其顶点坐标为(2,-2),
故可设其函数关系式为:S=a(t-2)2-2.
∵所求函数关系式的图象过(0,0),
于是得:
a(0-2)2-2=0,
解得a=
.
∴所求函数关系式为:S=
(t-2)2-2,即S=
t2-2t.
答:累积利润S与时间t之间的函数关系式为:S=
t2-2t;
(2)把S=30代入S=
(t-2)2-2,
得
(t-2)2-2=30.
解得t1=10,t2=-6(舍去).
答:截止到10月末公司累积利润可达30万元.
(3)把t=7代入关系式,
得S=
×72-2×7=10.5,
把t=8代入关系式,
得S=
×82-2×8=16,
16-10.5=5.5,
答:第8个月公司所获利是5.5万元.
故可设其函数关系式为:S=a(t-2)2-2.
∵所求函数关系式的图象过(0,0),
于是得:
a(0-2)2-2=0,
解得a=
| 1 |
| 2 |
∴所求函数关系式为:S=
| 1 |
| 2 |
| 1 |
| 2 |
答:累积利润S与时间t之间的函数关系式为:S=
| 1 |
| 2 |
(2)把S=30代入S=
| 1 |
| 2 |
得
| 1 |
| 2 |
解得t1=10,t2=-6(舍去).
答:截止到10月末公司累积利润可达30万元.
(3)把t=7代入关系式,
得S=
| 1 |
| 2 |
把t=8代入关系式,
得S=
| 1 |
| 2 |
16-10.5=5.5,
答:第8个月公司所获利是5.5万元.
点评:此题主要考查了二次函数的性质在实际生活中的应用,我们首先要吃透题意,确定变量,建立函数模型,尤其是对本题图象中所给的信息是解决问题的关键.

练习册系列答案
相关题目
| 3 | 8 |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、±2
|
 如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由.
如图,∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,∠COE的度数是∠AOB的度数的2倍吗?如果是,请说明理由.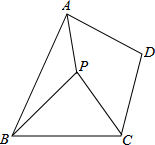 在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.
在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.
 如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数.
如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数.