题目内容
 如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.
如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.考点:两点间的距离
专题:
分析:先根据点M,N分别是AC、BC的中点得出MC=
AC,NC=
BC,再根据MN=MC+NC即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵点M,N分别是AC、BC的中点,AB=acm,
∴MC=
AC,NC=
BC,
∴MN=MC+NC=
(AC+BC)=
AB=
a(cm).
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=MC+NC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
四边形ABCD中,AD∥BC,要判定ABCD是平行四边形,那么还需满足( )
| A、∠B+∠C=180° |
| B、∠B+∠D=180° |
| C、∠A+∠B=180° |
| D、∠A+∠D=180° |
下列各对数中,数值相等的是( )
| A、-32与-23 |
| B、(-3)2与-32 |
| C、-23与(-2)3 |
| D、(-3×2)3与-3×23 |
如果上升3米记作“+3”米,那么下降2米记作( )米.
| A、-2 | B、+5 | C、-5 | D、+2 |
 如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为
如图:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的高为
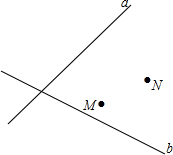 (1)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹;
(1)a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留作图痕迹;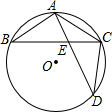 如图,在⊙O中,
如图,在⊙O中,