题目内容
四边形ABCD中,AD∥BC,要判定ABCD是平行四边形,那么还需满足( )
| A、∠B+∠C=180° |
| B、∠B+∠D=180° |
| C、∠A+∠B=180° |
| D、∠A+∠D=180° |
考点:平行四边形的判定
专题:
分析:根据平行四边形的5种判定方法分别进行分析即可.
解答: 解:∵四边形ABCD中,AD∥BC,
解:∵四边形ABCD中,AD∥BC,
∴要想成为平行四边形还需AB∥CD,
∴当∠B+∠C=180°时,AB∥CD,
故选A.
 解:∵四边形ABCD中,AD∥BC,
解:∵四边形ABCD中,AD∥BC,∴要想成为平行四边形还需AB∥CD,
∴当∠B+∠C=180°时,AB∥CD,
故选A.
点评:此题主要考查学生对平行四边形的判定的掌握情况.平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目
下列运算正确的是( )
| A、(-2a2)3=-8a6 |
| B、a-2a=a |
| C、a6-a3=a2 |
| D、(a+b)2=a2+b2 |
在下列实数中,无理数是( )
A、
| ||
B、
| ||
C、-
| ||
| D、0 |
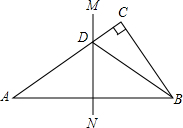 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )
如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若BC=4cm,则BD的长为( )| A、4cm | B、5cm |
| C、6cm | D、7cm |
 如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.
如图,点C在线段AB上,AB=acm,点MN分别是AC、BC的中点,求线段MN的长.