题目内容
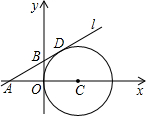 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求:
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求:(1)点D的坐标;
(2)直线l的解析式.
考点:切线的性质,待定系数法求一次函数解析式
专题:
分析:(1)连接CD,由于直线l为⊙C的切线,故CD⊥AD.C点坐标为(1,0),故OC=1,即⊙C的半径为1,由点A的坐标为(-1,0),可求出∠CAD=30度.作DE⊥AC于E点,则∠CDE=∠CAD=30°,可求出CE,进而得出OE,DE,得出点D的坐标.
(2)设直线l的函数解析式为y=kx+b,把A,D两点的坐标代入即可求出未知数的值从而求出其解析式.
(2)设直线l的函数解析式为y=kx+b,把A,D两点的坐标代入即可求出未知数的值从而求出其解析式.
解答: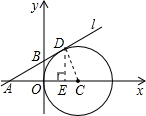 解:(1)如图所示,当直线l在x轴的上方时,
解:(1)如图所示,当直线l在x轴的上方时,
连接CD,
∵直线l为⊙C的切线,
∴CD⊥AD.
∵C点坐标为(1,0),
∴OC=1,即⊙C的半径为1,
∴CD=OC=1.
又∵点A的坐标为(-1,0),
∴AC=2,
∴∠CAD=30°,
∴AD=
,DE=
,AE=
,
∴OE=
,
∴D(
,
),
(2)设直线l解析式为:y=kx+b(k≠0),则,
解得k=
,b=
,
∴直线l的函数解析式为y=
x+
.
同理可得,当直线l在x轴的下方时,直线l的函数解析式为y=-
x-
.
故直线l的函数解析式为y=
x+
或y=-
x-
.
 解:(1)如图所示,当直线l在x轴的上方时,
解:(1)如图所示,当直线l在x轴的上方时,连接CD,
∵直线l为⊙C的切线,
∴CD⊥AD.
∵C点坐标为(1,0),
∴OC=1,即⊙C的半径为1,
∴CD=OC=1.
又∵点A的坐标为(-1,0),
∴AC=2,
∴∠CAD=30°,
∴AD=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴OE=
| 1 |
| 2 |
∴D(
| 1 |
| 2 |
| ||
| 2 |
(2)设直线l解析式为:y=kx+b(k≠0),则,
解得k=
| ||
| 3 |
| ||
| 3 |
∴直线l的函数解析式为y=
| ||
| 3 |
| ||
| 3 |
同理可得,当直线l在x轴的下方时,直线l的函数解析式为y=-
| ||
| 3 |
| ||
| 3 |
故直线l的函数解析式为y=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题把求一次函数的解析式与圆的性质相结合,增加了题目的难度,解答此题的关键是作出辅助线,构造出直角三角形,利用解直角三角形的知识解答.

练习册系列答案
相关题目
在数轴上表示不等式x≥-2的解集,正确的是( )
A、 |
B、 |
C、 |
D、 |
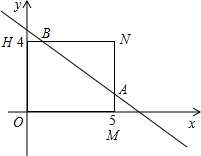 已知一动点P(x,y)在矩形OMNH内随机运动,其中O(0,0),M(5,0),N(5,4),H(0,4),直线y=-
已知一动点P(x,y)在矩形OMNH内随机运动,其中O(0,0),M(5,0),N(5,4),H(0,4),直线y=-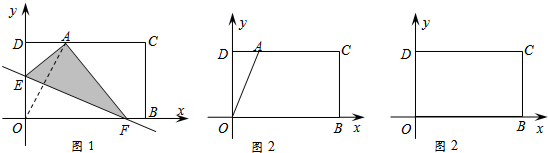
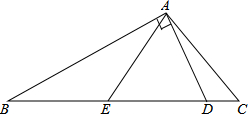 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.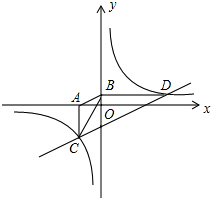 如图,已知双曲线y=
如图,已知双曲线y=