题目内容
用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量C及购买这两种原料的价格如下表:
(1)现配制这种饮料10千克,要求至少含有4200单位的维生素C,求至少需要甲原料多少千克?
(2)如果还需要购买甲、乙两种原料的费用不超过72元,求至少需要甲原料多少千克?
| 原料 维生素及价格 | 甲 | 乙 |
| 维生素C(单位/千克) | 600 | 100 |
| 原料价格(元/千克) | 8 | 4 |
(2)如果还需要购买甲、乙两种原料的费用不超过72元,求至少需要甲原料多少千克?
考点:一元一次不等式的应用
专题:
分析:(1)设所需甲种原料的质量为x千克,首先由甲种原料所需的质量和饮料的总质量,表示出乙种原料的质量,再结合表格中的数据,根据“至少含有4200单位的维生素C”这一不等关系列不等式,解不等式;
(2)根据购买甲、乙两种原料的费用不超过72元,列不等式求解.
(2)根据购买甲、乙两种原料的费用不超过72元,列不等式求解.
解答:解:(1)设所需甲种原料的质量为xkg,则需乙种原料(10-x)kg.
根据题意,得:600x+100(10-x)≥4200,
解得:x≥6.4,
答:至少需要甲原料6.4千克;
(2)由题意得,8x+4(10-x)≤72,
解得:x≤8,
由(1)得:x≥6.4,
则6.4≤x≤8,
答:至少需要甲原料6.4千克.
根据题意,得:600x+100(10-x)≥4200,
解得:x≥6.4,
答:至少需要甲原料6.4千克;
(2)由题意得,8x+4(10-x)≤72,
解得:x≤8,
由(1)得:x≥6.4,
则6.4≤x≤8,
答:至少需要甲原料6.4千克.
点评:此题主要考查了一元一次不等式的应用,解答本题的关键是仔细审题,建立数学模型,将实际问题转变为数学问题求解.

练习册系列答案
相关题目
方程组
的解与x与y的值相等,则k等于( )
|
| A、1 | B、-1 | C、2 | D、-2 |
 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.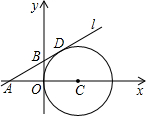 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求:
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求: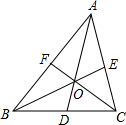 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.