题目内容
阅读下列材料:
问题:在平面直角坐标系xOy中,一张矩形纸片OBCD按图1所示放置.已知OB=10,BC=6,将这张纸片折叠,使点O落在边CD上,记作点A,折痕与边OD(含端点)交于点E,与边OB(含端点)或其延长线交于点F,求点A的坐标.
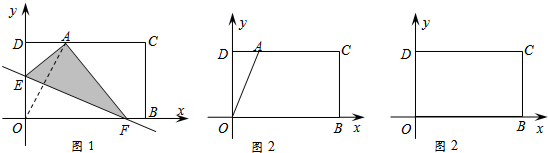
小明在解决这个问题时发现:要求点A的坐标,只要求出线段AD的长即可,连接OA,设折痕EF所在直线对应的函数表达式为:y=kx+n(k<0,n≥0),于是有E(0,n),F(-
,0),所以在Rt△EOF中,得到tan∠OFE=-k,在Rt△AOD中,利用等角的三角函数值相等,就可以求出线段DA的长(如图1)
请回答:
(1)如图1,若点E的坐标为(0,4),直接写出点A的坐标;
(2)在图2中,已知点O落在边CD上的点A处,请画出折痕所在的直线EF(要求:尺规作图,保留作图痕迹,不写做法);
参考小明的做法,解决以下问题:
(3)将矩形沿直线y=-
x+n折叠,求点A的坐标;
(4)将矩形沿直线y=kx+n折叠,点F在边OB上(含端点),直接写出k的取值范围.
问题:在平面直角坐标系xOy中,一张矩形纸片OBCD按图1所示放置.已知OB=10,BC=6,将这张纸片折叠,使点O落在边CD上,记作点A,折痕与边OD(含端点)交于点E,与边OB(含端点)或其延长线交于点F,求点A的坐标.

小明在解决这个问题时发现:要求点A的坐标,只要求出线段AD的长即可,连接OA,设折痕EF所在直线对应的函数表达式为:y=kx+n(k<0,n≥0),于是有E(0,n),F(-
| n |
| k |
请回答:
(1)如图1,若点E的坐标为(0,4),直接写出点A的坐标;
(2)在图2中,已知点O落在边CD上的点A处,请画出折痕所在的直线EF(要求:尺规作图,保留作图痕迹,不写做法);
参考小明的做法,解决以下问题:
(3)将矩形沿直线y=-
| 1 |
| 2 |
(4)将矩形沿直线y=kx+n折叠,点F在边OB上(含端点),直接写出k的取值范围.
考点:一次函数综合题
专题:
分析:(1)如图1,在Rt△EOF中,得到tan∠OFE=-k,在Rt△AOD中,利用等角的三角函数值相等,就可以求出线段DA的长;
(2)作OA的中垂线即可;
(3)如图,设直线y=-
x+n,则E点的坐标为(0,n),F点的坐标为(2n,0),OE=n,OF=2n,由△AEF≌△OEF可知OE=AE=n,AF=OF=2n,由∠EAF=90°可知∠1+∠3=90°,从而求得∠1=∠2,得出△DEA∽△GAF所以
=
,由FG=CB=6解得DA=3,从而求得A点的坐标.
(4)根据图象和矩形的边长可直接得出k的取值范围,
(2)作OA的中垂线即可;
(3)如图,设直线y=-
| 1 |
| 2 |
| AE |
| FA |
| DA |
| GF |
(4)根据图象和矩形的边长可直接得出k的取值范围,
解答:解:(1)如图1若点E的坐标为(0,4),直接写出点A的坐标为(2
,6);
(2)如图所示:

(3)如图,过的F作FG⊥DC于G
∵EF解析式为y=-
x+n,
∴E点的坐标为(0,n),
∴OE=n
∴F点的坐标为(2n,0),
∴OF=2n
∵△AEF与△OEF全等,
∴OE=AE=n,AF=OF=2n
∵点A在DC上,且∠EAF=90°
∴∠1+∠3=90°
又∵∠3+∠2=90°
∴∠1=∠2
在△DEA与△GAF中,
∴△DEA∽△GAF(AA)
∴
=
∵FG=CB=6
∴
=
∴DA=3
∴A点的坐标为(3,6).

(4)-1≤k≤-
.
∵矩形沿直线y=kx+n折叠,点F在边OB上,(1)当E点和D点重合时,k的值为-1,(2)当F点和B点重合时,k的值为-
;

∴-1≤k≤-
.
| 3 |
(2)如图所示:

(3)如图,过的F作FG⊥DC于G
∵EF解析式为y=-
| 1 |
| 2 |
∴E点的坐标为(0,n),
∴OE=n
∴F点的坐标为(2n,0),
∴OF=2n
∵△AEF与△OEF全等,
∴OE=AE=n,AF=OF=2n
∵点A在DC上,且∠EAF=90°
∴∠1+∠3=90°
又∵∠3+∠2=90°
∴∠1=∠2
在△DEA与△GAF中,
|
∴△DEA∽△GAF(AA)
∴
| AE |
| FA |
| DA |
| GF |
∵FG=CB=6
∴
| n |
| 2n |
| DA |
| 6 |
∴DA=3
∴A点的坐标为(3,6).

(4)-1≤k≤-
| 1 |
| 3 |
∵矩形沿直线y=kx+n折叠,点F在边OB上,(1)当E点和D点重合时,k的值为-1,(2)当F点和B点重合时,k的值为-
| 1 |
| 3 |

∴-1≤k≤-
| 1 |
| 3 |
点评:这是一道有关折叠的问题,主要考查一次函数、四边形、相似形等知识,试题中贯穿了方程思想和数形结合的思想,请注意体会.

练习册系列答案
相关题目
把分式
中的x和y都扩大为原来的3倍,那么分式的值( )
| x2 |
| 2x+y |
| A、不变 |
| B、扩大为原来的3倍 |
| C、扩大为原来的6倍 |
| D、扩大为原来的9倍 |

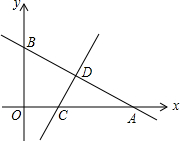 如图,一次函数y=kx+n的图象与x轴和y轴分别交于点A(6,0)和B(0,2
如图,一次函数y=kx+n的图象与x轴和y轴分别交于点A(6,0)和B(0,2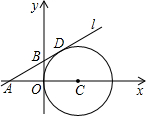 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求:
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求: 请写出点A,B,C,D,的坐标.
请写出点A,B,C,D,的坐标.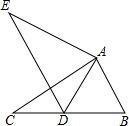 如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为