题目内容
2. 实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.
实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.
分析 首先利用数轴判断出:b<0,b-a<0,进而化简二次根式得出即可.
解答 解:由数轴可得:b<0,b-a<0,
则$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$=-b+b-a=-a.
故答案为:-a.
点评 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.

练习册系列答案
相关题目
10.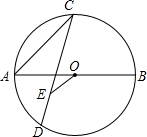 如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
 如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )| A. | $\sqrt{5}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{5}{3}$ |
17.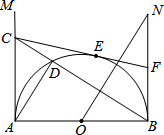 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )| A. | n=$\frac{1}{2}$ | B. | 0<n≤$\frac{3}{4}$ | C. | $\frac{1}{2}$≤n<1 | D. | 无法确定 |
14.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于$\frac{5}{4}$n2,则算过关;否则不算过关,则能过第2关的概率是( )
| A. | $\frac{13}{18}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
 如图,M是平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形.
如图,M是平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形.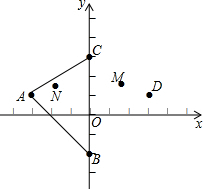 在图中,三角形DBC是由三角形ABC经过某种变换后得到的图形,分别写出点A、B、C、D的坐标.观察点A与点D的坐标之间的关系,如果三角形ABC中任一点N的坐标为N(x,y),它的对应点M的坐标是什么?
在图中,三角形DBC是由三角形ABC经过某种变换后得到的图形,分别写出点A、B、C、D的坐标.观察点A与点D的坐标之间的关系,如果三角形ABC中任一点N的坐标为N(x,y),它的对应点M的坐标是什么? 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标为($\frac{3}{2}$,3).