题目内容
14.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于$\frac{5}{4}$n2,则算过关;否则不算过关,则能过第2关的概率是( )| A. | $\frac{13}{18}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能过第2关的情况,再利用概率公式即可求得答案.
解答 解:∵过第2关的抛掷所出现的点数之和大于$\frac{5}{4}$n2=$\frac{5}{4}$×22=5,
列表得:
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 |
∴能过第2关的概率是:$\frac{26}{36}$=$\frac{13}{18}$.
故选A.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
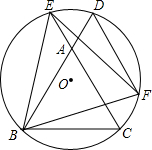 如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.
如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由. 实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.
实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.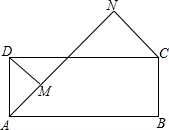 如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.
如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.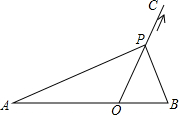 如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$.
如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$. 在如图中以点P为位似中心,画一个三角形,与原三角形位似,使它与原三角形的位似比是1:2.
在如图中以点P为位似中心,画一个三角形,与原三角形位似,使它与原三角形的位似比是1:2.