题目内容
17.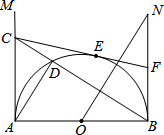 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )| A. | n=$\frac{1}{2}$ | B. | 0<n≤$\frac{3}{4}$ | C. | $\frac{1}{2}$≤n<1 | D. | 无法确定 |
分析 作FH⊥AC于H,如图,设BN=1,则BF=n,半圆的半径为r,根据切线的性质得∠MAB=∠NBA=90°,易得四边形ABFH为矩形,所以HF=2r,AH=BF=n,再根据切线长定理得到CE=CA,FE=FB=n,设CA=t,则CE=t,CH=t-AH=t-n,在Rt△CHF中利用勾股定理得(t-n)2+(2r)2=(t+n)2,解得t=$\frac{{r}^{2}}{n}$,接着证明Rt△BON∽Rt△ACB,然后利用相似比得可计算出n=$\frac{1}{2}$.
解答 解:作FH⊥AC于H,如图, 设BN=1,则BF=n,半圆的半径为r,
设BN=1,则BF=n,半圆的半径为r,
∵AM、BN为半圆的切线,
∴∠MAB=∠NBA=90°,
∴四边形ABFH为矩形,
∴HF=2r,AH=BF=n,
∵CF切半圆于E点,
∴CE=CA,FE=FB=n,
设CA=t,则CE=t,CH=t-AH=t-n,
在Rt△CHF中,∵CH2+FH2=CF2,
∴(t-n)2+(2r)2=(t+n)2,解得t=$\frac{{r}^{2}}{n}$,
∵AB是半圆O的直径,
∴∠ADB=90°,
∵ON⊥BD,
∴AD∥ON,
∴∠BON=∠BAD,
∵∠BAD+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BAD=∠ACD,
∴∠BON=∠ACB,
∴Rt△BON∽Rt△ACB,
∴$\frac{OB}{AC}$=$\frac{BN}{AB}$,即$\frac{r}{\frac{{r}^{2}}{n}}$=$\frac{1}{2r}$,
∴n=$\frac{1}{2}$.
故选A.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、切线的性质和切线长定理;会运用相似比和勾股定理计算线段的长.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
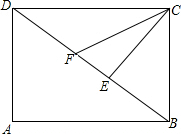 如图,已知平行四边形ABCD中,∠BCD=90°,CE⊥BD于E,CF平分∠DCE与DB交于点F,
如图,已知平行四边形ABCD中,∠BCD=90°,CE⊥BD于E,CF平分∠DCE与DB交于点F,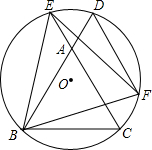 如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.
如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.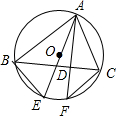 已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF, 实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.
实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.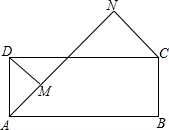 如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm.
如图,矩形ABCD中,AB>AD,AB=10cm,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,则DM+CN=5$\sqrt{2}$cm. 在如图中以点P为位似中心,画一个三角形,与原三角形位似,使它与原三角形的位似比是1:2.
在如图中以点P为位似中心,画一个三角形,与原三角形位似,使它与原三角形的位似比是1:2.