题目内容
10.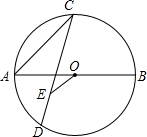 如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )
如图,AB是⊙O的直径,点C是半圆的中点,连接AC,CD是弦.若AB=10,tan∠ACD=$\frac{3}{4}$,CA=CE,连接OE,则OE的长为( )| A. | $\sqrt{5}$ | B. | $\frac{5}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{5}{3}$ |
分析 连接AE,作EM⊥AD,EF⊥BD,ON⊥BD垂足为M,F,N,EK⊥ON垂足为K,由AC弧=BC弧,AB是直径,得出∠CAO=∠ADC=CDB=45°,∠DAE=∠EAO,从而证得E是三角形的内心,求得EF=2,ON=3,KN=2,EK=2,求得EK=1,根据勾股定理即可求得OE的长.
解答 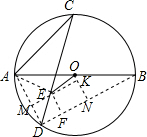 解:连接AE,作EM⊥AD,EF⊥BD,ON⊥BD垂足为M,F,N,EK⊥ON垂足为K,
解:连接AE,作EM⊥AD,EF⊥BD,ON⊥BD垂足为M,F,N,EK⊥ON垂足为K,
∵CA=CE,
∴∠CAE=∠CEA,
∵∠CEA=∠DAE+∠EDA,
∴∠CAO+∠OAE=∠DAE+∠ADE,
∵AC弧=BC弧,AB是直径,
∴∠CAO=∠ADC=CDB=45°,
∴∠DAE=∠EAO,
∴E是三角形的内心,
∵tan∠ACD=$\frac{3}{4}$,∠ACD=∠ABD,
∴tan∠ABD=$\frac{3}{4}$,
∵AB=10,
∴AD=6,BD=8,
∴内切圆的半径EF=2,
易知ON=3,KN=2,EK=2,
∴OK=1,
在RT△OEK中OE=$\sqrt{O{K}^{2}+E{K}^{2}}$=$\sqrt{5}$.
故选A.
点评 本题考查了垂径定理,圆周角定理,勾股定理,三角形的内切圆的判定和性质,解直角三角形等,证得E是三角形ABD的内心是解题的关键.

练习册系列答案
相关题目
6.“五一”节日期间,某超市进行积分兑换活动,具体兑换方法见右表,爸爸拿出自己的积分卡,对小华说“这里积有7000分,你去给咱家兑换礼品吧,”小华兑换了两种礼品,共5件,并刚好用完积分,请问她兑换了哪两种礼品,各多少件?
| 积分兑换礼品表 | |
| 兑换礼品 | 积分 |
| MP3一个 | 3000分 |
| 电茶壶一个 | 2000分 |
| 书包一个 | 1000分 |
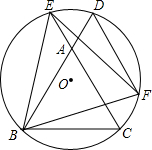 如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.
如图,△ABC是等边三角形,⊙O过B、C两点,与BA、CA的延长线分别交于点D、E,弦DF∥AC交⊙O于点F,连结BE、BF、EF.试判断△BEF的形状,并说明理由.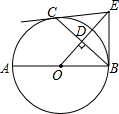 如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE. 实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.
实数a,b在数轴上的位置如图所示,且|b|>|a|,则化简$\sqrt{{b}^{2}}$-$\sqrt{(b-a)^{2}}$的结果为-a.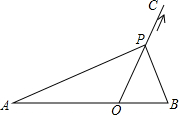 如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$.
如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t秒,当△ABP是直角三角形时,t的值为1或$\frac{-1+\sqrt{33}}{8}$.