题目内容
6.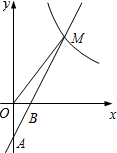 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.(1)求一次函数和反比例函数的解析式;
(2)若点P是x轴正半轴上一点且∠AMP=90°,求点P的坐标.
分析 (1)把A、B两点代入y=kx+b即可求出一次函数解析式,根据面积求出点M坐标,即可求出反比例函数解析式.
(2)由△OAB∽△MPB,利用相似三角形的性质求出PB即可.
解答 解:(1)∵一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,
∴$\left\{\begin{array}{l}k+b=0\\ b=-2\end{array}\right.$ 解得$\left\{\begin{array}{l}k=2\\ b=-2\end{array}\right.$,
∴一次函数的解析式为y=2x-2,
设点M的坐标为(x,2x-2),
∵△OBM的面积是2,M在第一象限内,
∴$\frac{1}{2}$×1×(2x-2)=2
∴x=3,
∴M(3,4),
∵点M(3,4)在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,
∴m=12,
∴反比例函数的解析式为y=$\frac{12}{x}$.
(2)∵A(0,-2),B(1,0),O(0,0),M(3,4),
∴OB=1,AB=$\sqrt{1+(-2)^{2}}$=$\sqrt{5}$,MB=$\sqrt{(3-1)^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵∠AOB=∠AMP=90°,
∠OBA=∠MBP,
∴△OAB∽△MPB,
∴$\frac{OB}{BM}=\frac{AB}{BP}$,
∴BP=10,
∴P(11,0).
点评 本题考查一次函数以及反比例函数的有关性质,学会待定系数法确定函数的解析式,解题的关键是利用相似三角形的性质解决问题的,属于中考常考题型.

练习册系列答案
相关题目
17. 如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )
 如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:| 2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
| 参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
| 右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
| 频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
| A. | 0.6 | B. | 0.5 | C. | 0.45 | D. | 0.4 |
1.崇明县校园足球运动正在蓬勃发展,已知某校学生“足球社团”成员的年龄与人数情况如下表所示:那么“足球社团”成员年龄的中位数是14岁.
| 年龄(岁) | 11 | 12 | 13 | 14 | 15 |
| 人数 | 3 | 3 | 7 | 12 | 14 |
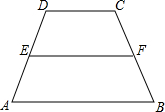 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).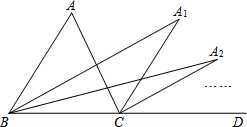 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.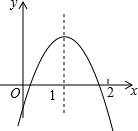 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论: