题目内容
13.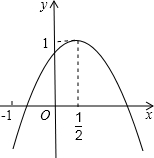 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据二次函数图象反映出的数量关系,逐一判断正确性.
解答 解:根据图象可知:
①a<0,c>0
∴ac<0,正确;
②∵顶点坐标横坐标等于0.5,
∴-$\frac{b}{2a}$=$\frac{1}{2}$,
∴a+b=0正确;
③∵顶点坐标纵坐标为1,
∴$\frac{4ac-{b}^{2}}{4a}$=1;
∴4ac-b2=4a,正确;
④当x=1时,y=a+b+c>0,
当x=-1时,y=a-b+c<0,
则(a-b+c)(a+b+c)<0,即(a+c)2-b2<0,正确.
正确的有4个.
故选D.
点评 本题主要考查了二次函数的性质,会根据图象获取所需要的信息.掌握函数性质灵活运用.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | a5+a5=a10 | B. | a6×a4=a24 | C. | a4÷a3=a | D. | a4-a4=a0 |
8.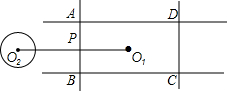 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
18.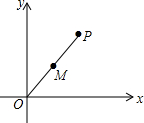 如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )
如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )
①点O在⊙P外;②点M在⊙P上;③x轴与⊙P相离;④y轴与⊙P相切.
 如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )
如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )①点O在⊙P外;②点M在⊙P上;③x轴与⊙P相离;④y轴与⊙P相切.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若代数式3x2-2x+1与-x2+5x-3的值互为相反数,则x的值为( )
| A. | -$\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或2 | C. | -2或$\frac{1}{2}$ | D. | -$\frac{1}{2}$或2 |
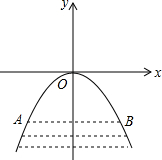 某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
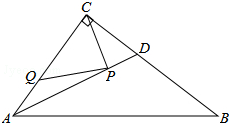 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是$\frac{24}{5}$.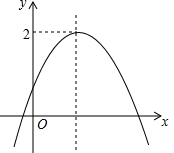 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论: