题目内容
18.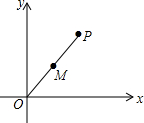 如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )
如图,平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作⊙P,则下列判断正确的有( )①点O在⊙P外;②点M在⊙P上;③x轴与⊙P相离;④y轴与⊙P相切.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 过P点作PA⊥x轴于A,作PB⊥y轴于B,根据勾股定理可求OP,根据中点的定义可得PM,再根据点与圆的位置关系,直线与圆的位置关系即可求解.
解答  解:过P点作PA⊥x轴于A,作PB⊥y轴于B,
解:过P点作PA⊥x轴于A,作PB⊥y轴于B,
∵P(6,8),
∴PA=8,PB=6,
在Rt△OAP中,根据勾股定理可得OP=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵M为OP中点,
∴PM=5,
∵⊙P的半径是6,
∴①点O在⊙P外;
②点M在⊙P内;
③x轴与⊙P相离;
④y轴与⊙P相切.
故正确的有3个.
故选:C.
点评 本题考查了直线和圆的位置关系,坐标与图形性质,点与圆的位置关系,直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理的知识.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
9.当代数式x2+3x+8的值等于7时,代数式3x2+9x-2的值等于( )
| A. | 5 | B. | 3 | C. | -2 | D. | -5 |
13.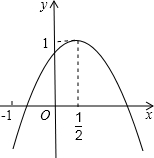 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )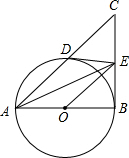 如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
如图,△ABC中∠ABC=90°,以AB为直径作⊙O,与AC交于点D,点E为DC中点,连DE
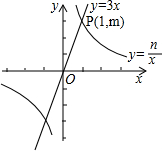 如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.
如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1. 已知:△ABC.
已知:△ABC.