题目内容
2.若代数式3x2-2x+1与-x2+5x-3的值互为相反数,则x的值为( )| A. | -$\frac{1}{2}$或-2 | B. | $\frac{1}{2}$或2 | C. | -2或$\frac{1}{2}$ | D. | -$\frac{1}{2}$或2 |
分析 利用互为相反数两数之和为0列出方程,求出方程的解即可得到x的值.
解答 解:根据题意得:3x2-2x+1-x2+5x-3=0,
整理得:2x2+3x-2=0,
分解因式得:(2x-1)(x+2)=0.
解得:x=$\frac{1}{2}$或x=-2,
故选C
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
13.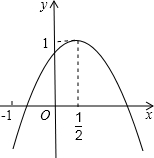 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.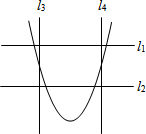 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.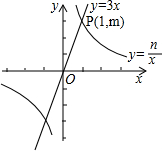 如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1.
如图,在平面直角坐标系xOy中,直线y=3x与双曲线y=$\frac{n}{x}$(n≠0)在第一象限的公共点是P(1,m).小明说:“从图象上可以看出,满足3x>$\frac{n}{x}$的x的取值范围是x>1.”你同意他的观点吗?答:不正确.理由是x的取值范围是-1<x<0或x>1. 已知:△ABC.
已知:△ABC.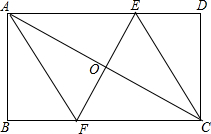 如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.
如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.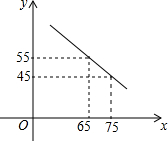 某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.
某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.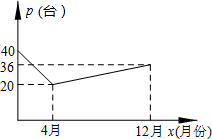 由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=$\left\{\begin{array}{l}-0.05x+0.4(1≤x<4)\\ 0.2(4≤x≤12\end{array})$,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.