题目内容
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b],对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k>0)是闭区间[m,n]上的“闭函数”,求此函数的解析式.
(1)反比例函数y=
| 2015 |
| x |
(2)若一次函数y=kx+b(k>0)是闭区间[m,n]上的“闭函数”,求此函数的解析式.
考点:反比例函数的性质,一次函数的性质
专题:新定义
分析:(1)根据反比例函数y=
的单调区间进行判断;
(2)根据新定义运算法则列出关于系数k、b的方程组
,通过解该方程组即可求得系数k、b的值.
| 2015 |
| x |
(2)根据新定义运算法则列出关于系数k、b的方程组
|
解答:解:(1)反比例函数y=
是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=
在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
所以,当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,故
反比例函数y=
是闭区间[1,2015]上的“闭函数”;
(2)∵k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,
∴
,
解得
.
∴此函数的解析式是y=x.
| 2015 |
| x |
反比例函数y=
| 2015 |
| x |
当x=1时,y=2015;
当x=2015时,y=1,
所以,当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,故
反比例函数y=
| 2015 |
| x |
(2)∵k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,
∴
|
解得
|
∴此函数的解析式是y=x.
点评:本题考查的是反比例函数的性质,解题的关键是弄清楚“闭函数”的定义.解题时,也要注意“分类讨论”数学思想的应用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
有理数a、b在数轴上的位置如图所示,则把a,-a,b,-b按照从小到大的顺序排列正确的是( )


| A、-a<-b<a<b |
| B、-b<a<-a<b |
| C、-b<-a<a<b |
| D、-b<b<-a<a |
一工厂生产销售某种电子产品,11月份销售电子产品的利润(每台电子产品的利润=出厂价-成本)是出厂价的30%;12月将每台电子产品的出厂价调低5%(每台电子产品的成本不变),销售件数比11月增加44%,那么该厂12月份销售这种电子产品的利润总额将比11月份利润总额增长( )
| A、10% | B、15% |
| C、20% | D、25% |
关于函数y=
,下列说法正确的是( )
| 2 |
| x |
| A、函数图象关于原点对称 |
| B、函数图象关于x轴对称 |
| C、函数图象关于y轴对称 |
| D、y的值随x值的增大而减小 |
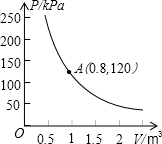 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )| A、小于0.64m3 |
| B、大于0.64m3 |
| C、不小于0.64m3 |
| D、不大于0.64m3 |
我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“有100个和尚分100只馒头正好分完.如果大和尚一人分3只小和尚3人分一只,试问大、小和尚各有几人?”请算算大和尚有( )
| A、25人 | B、30人 |
| C、50人 | D、75人 |
下列实数中是无理数的是( )
A、
| ||
| B、π | ||
| C、0.141414 | ||
D、-
|
 已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC.
已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC. 如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是
如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是