题目内容
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )| A. | 与x轴有两个公共点; | |
| B. | 与y轴的交点坐标是(0,3); | |
| C. | 当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小; | |
| D. | 开口向上. |
分析 根据二次函数的解析式结合二次函数的性质,逐一分析四个选项的正误即可得出结论.
解答 解:A、在方程-x2+2x-3=0中,
△=22-4×(-1)×(-3)=-8<0,
∴抛物线y=-x2+2x-3与x轴无交点,A错误;
B、当x=0时,y=-3,
∴抛物线y=-x2+2x-3与y轴的交点坐标为(0,-3),B错误;
C、抛物线y=-x2+2x-3=-(x-1)2-2,
∴该抛物线的对称轴为x=1,
∵a=-1<0,
∴当x<1时y随x的增大而增大,当x>1时y随x的增大而减小.C正确;
D、在抛物线y=-x2+2x-3中a=-1<0,
∴抛物线y=-x2+2x-3开口向下,D错误.
故选C.
点评 本题考查了二次函数的性质以及二次函数图象与系数的关系,熟练掌握二次函数图象与系数之间的关系是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
14.一元二次方程5x2-11x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
15. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )| A. | 两根都大于0 | B. | 两根都等于0 | ||
| C. | 两根都小于0 | D. | 一根大于0,一根小于0 |
12. 如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
 如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
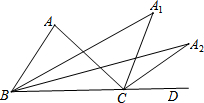 如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
如图,在△ABC中,∠A=96°,延长BC至D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )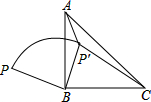 如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为1:2.
如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为1:2.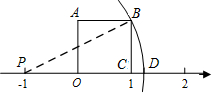 如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1.
如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1. 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )