题目内容
7.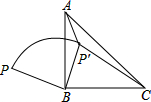 如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为1:2.
如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为1:2.
分析 如图,连接AP,构建全等三角形:△ABP≌△CBP′(SAS),由该全等三角形的对应边相等得到AP=P′C;如图,连接PP′,结合已知条件可以推知△APP′是直角三角形,所以由勾股定理来求相关线段的长度即可.
解答 解: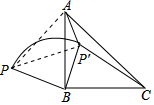 如图,连接AP,
如图,连接AP,
∵BP绕点B顺时针旋转90°到BP′,
∴BP=BP′,∠ABP+∠ABP′=90°,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=90°,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
∵$\left\{\begin{array}{l}{BP=BP′}\\{∠ABP=∠CBP′}\\{AB=BC}\end{array}\right.$,
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
连接PP′,则△PBP′是等腰直角三角形,
∴∠BP′P=45°,PP′=$\sqrt{2}$PB,
∵∠AP′B=135°,
∴∠AP′P=135°-45°=90°,
∴△APP′是直角三角形,
设P′A=x,则AP=3x,
根据勾股定理,PP′=$\sqrt{A{P}^{2}-P′{A}^{2}}$=$\sqrt{(3x)^{2}-{x}^{2}}$=2$\sqrt{2}$x,
∴PP′=$\sqrt{2}$PB=2$\sqrt{2}$x,
解得PB=2x,
∴P′A:PB=x:2x=1:2.
故答案是:1:2.
点评 本题考查了旋转的性质和等腰直角三角形的性质,根据题意作出辅助线是解题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.用代数式表示“m的3倍与n的平方差”,正确的是( )
| A. | (3m-n)2 | B. | 3(m-n)2 | C. | (3m)2-n2 | D. | (m-3n)2 |
17.△ABC的三条外角平分线相交成一个△A′B′C′,则△A′B′C′( )
| A. | 一定是钝角三角形 | B. | 一定是直角三角形 | ||
| C. | 一定是锐角三角形 | D. | 一定不是锐角三角形 |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个公共点; | |
| B. | 与y轴的交点坐标是(0,3); | |
| C. | 当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小; | |
| D. | 开口向上. |
 中自变量
中自变量 的取值范围是__________________.
的取值范围是__________________. 如图,在△ABC中,点D是AB上的一点,作DE∥BC交AC于点E,连接CD、BE交于点G,取BC的中点F,并连接FG,则图中三角形面积一定相等的有( )
如图,在△ABC中,点D是AB上的一点,作DE∥BC交AC于点E,连接CD、BE交于点G,取BC的中点F,并连接FG,则图中三角形面积一定相等的有( )